Vì sao chơi poker giúp bạn tư duy chiến lược tốt hơn cờ vua? Tất tần tật về Thiên Nga Đen
Mấy bữa nay người viết có dịp đọc lại 2 cuốn sách kinh điển của bác Nassim Taleb là Thiên Nga Đen và Khả năng cải thiện nghịch cảnh....
Mấy bữa nay người viết có dịp đọc lại 2 cuốn sách kinh điển của bác Nassim Taleb là Thiên Nga Đen và Khả năng cải thiện nghịch cảnh. Sự bất định và tư duy chiến lược là hai chủ đề rất thú vị, và khá giống với hai mặt của đồng xu. Khi đã suy nghĩ về một chủ đề, không sớm thì muộn đọc giả cũng phải suy nghĩ về chủ đề kia.
Chưa có một tác giả nào có đóng góp về kiến thức xác xuất cho công chúng nhiều như bác Nassim Taleb. Trong cộng đồng tri thức, tên của bác này được kính nể với sự tôn trọng hết mức. Tuy nhiên, với những bạn đã quen thuộc sách của bác này thì hàm lượng câu từ chửi xéo văng tục cũng nhiều không kém những ý tưởng tuyệt vời trong từng trang sách. Fan cuồng bác này không ít, tuy nhiên kẻ thù phải gấp vài lần, nhưng có 1 điều không ai có thể phủ nhận là bác Taleb có những suy nghĩ rất sâu sắc về rủi ro, xác xuất, và tư duy chiến lược. Taleb có thể rất ngạo mạn, nhưng ông rất thông minh.
Taleb đã cho người viết rất nhiều tư liệu thô để trầm ngâm về rủi ro và xác xuất. Trong 1 lần tác giả lướt qua các bài viết trước đây của mình, người viết nhận ra rằng có rất nhiều bài viết liên quan, trực tiếp hay gián tiếp, đến các ý tưởng của bác Taleb. Điều gì phải đến sẽ đến, định mệnh đã vẫy gọi người viết phải xâu chuỗi các bài viết trước đây thành 1 bức tranh tổng thể. Bài viết này là kết quả của quá trình tổng hợp đó, người viết sẽ đưa link của các bài viết trước vào để làm nền tảng cho cuộc thảo luận dưới đây. Bài viết này có rất nhiều khái niệm cứng đòi hỏi đọc giả phải quen thuộc với chủ đề, nên đọc trước các bài viết sẽ giúp bạn hiểu rõ những quan điểm được liệt kê dưới đây. Bạn không cẩn phải đọc nếu đã quen thuộc với những ý này, nhưng với những bạn chưa tập đi, tập chạy sẽ té sấp mặt đấy.
Mọi người thường nghĩ rằng những người chơi giỏi cờ vua sẽ tinh thông chiến lược hơn người bình thường. Suy cho cùng, đó là môn thể thao trí tuệ, người chơi đấu trí với nhau để dồn ép đối phương vào thế bí. Poker thì sao nhỉ? Là cờ bạc, chắc chắn rồi. So sánh giữa một lĩnh vực cờ bạc giải trí với môn thể thao trí tuệ có vẻ khập khiễng, nhưng không hẳn. Cờ vua là môn thể thao bị hiểu lầm nhiều nhất, đặc biệt là về tư duy chiến lược, vì ta thường nghĩ kĩ năng học được khi chơi cờ vua có thể được áp dụng trong nhiều lĩnh vực đời sống, nhưng bài viết dưới đây sẽ giải thích chính một môn cờ bạc như poker, không phải cờ vua, mới dạy bạn những bài học quan trọng về quyết định chiến lược và phân tích rủi ro.

Đọc thêm:
Đóng góp của Vilfredo Pareto?
Quy luật được giấu kín quản trị thế giới
Có 1 quy luật quản trị thế giới mà ta đang sống. Quy luật tuy rất quan trọng nhưng bị che khuất tới mức mà gần như ngày nào ta cũng gặp kết quả của nó nhưng lại không thể nhìn thấy. Bộ não đã trả qua hàng vạn năm tiến hóa của ta không được xây dựng để dễ dàng nhận biết quy tắc hàm mũ. Vilfredo Pareto, không ai khác chính là cha đẻ của quy luật này .

Không có gì trêu người hơn đồ thị hàm mũ, đơn giản vì nó quá xấu, quá mất cân đối, quá thiếu thẫm mỹ, quá .... à...thôi. Nhưng 1 đồ thị như thế giải thích gần như tất cả mọi hiện tượng bất công trong xã hội. Một nhóm nhỏ đẳng cấp nắm trong tay 1 miếng bánh to đùng trong khi phần còn lại tranh nhau miếng bánh thừa. Nói theo Pareto, xấp xỉ 20% nguyên nhân ảnh hưởng đến 80% kết quả.
Nhưng nếu quy luật này quan trọng như thế, tại sao nó lại bị giấu kín khỏi thế giới?
Trong suốt cuộc đấu tranh sinh tồn của loài Homo sapiens, tổ tiên của ta hiểu rất rõ quy tắc của số học (là nền tảng toán học cơ bản + - x /). Ví dụ như nếu tổ tiên của ta học được rằng cần tốn 3 giờ để mài 1 hòn đá thành 1 cây dao, nếu ta cần 3 cây dao thì sẽ tốn xấp xỉ khoảng 9 giờ (hoặc 3 người cùng mài 1 lúc). Nếu có 1 tảng thịt lớn được mang về từ cuộc đi săn, có khoảng 100 người trong bộ lạc thì cần chia miếng thịt này thành 100 phần nếu không nổi loạn sẽ xảy ra (lớn bé thế nào thì xét theo vai vế), abc và xyz. Có thể hiểu 1 cách đơn giản là mối liên hệ giữa 2 biến bất kì luôn là 1 hằng số (sẽ có trường hợp xuất hiện biên độ dao động nhưng về cơ bản vẫn bị ràng buộc bởi quy luật hàm số). Quả thật, hầu hết mối liên hệ giữa 2 biến bất kì luôn tuân theo quy luật "số học" trong phần lớn thời gian lịch sử. Tuy nhiên, mọi thứ mang tính quan trọng trong xã hội ngày nay đều tuân theo quy luật hàm mũ. Ta rất giỏi làm toán nhẩm cộng trừ nhân chia nhưng khi phải tính nhẩm lũy kép thì bó tay.

Đọc thêm:
Lấy ví dụ thương vong trong chiến tranh. Trong phần lớn chiều dài chiến tranh trong lịch sử, thương vong của binh sĩ luôn tuân theo quy luật số học. Để tiêu diệt 10 vạn quân địch, ta cần xấp xỉ tương đương 10 vạn hoặc hơn nếu tướng ngu, nếu là thiên tài quân sự có thể chỉ cần 1-3 vạn. 300 chiến binh Sparta cho dù là tinh binh của những tinh binh, họ đơn giản là không thể chiến thắng cả đội quân Ba Tư. Đao kiếm cung tên có giới hạn của nó, cho dù bạn có là Trần Hưng Đạo hay Alexander Đại Đế thì cũng chỉ có thể đẩy giới hạn này đến điểm cực, không thể hoàn toàn phá bỏ nó, và giới hạn này chính là quy luật hàm số.

Mỹ chỉ cần 2 quả nguyên tử để làm được những điều mà tướng quân trong quá khứ phải tốn hàng vạn quân, và hoàn thành việc này trong tích tắc. Khi giới hạn hàm số bị phá bỏ, quy luật hàm mũ sẽ thay thế. Đây chính là kỉ nguyên ta đang sống. Nhưng do bộ não homo sapien đã tiến hóa trong giai đoạn quy luật hàm số từng thống trị, không khó hiểu khi ta khó nhận thức được những hệ quả của quy luật hàm mũ.
Một trong những hệ quả là do tính chất lũy thừa của hàm mũ, may mắn quan trọng hơn bạn nghĩ rất rất rất............................. rất nhiều. Lấy ví dụ 4^10 và 5^10, xuất phát điểm chỉ khác nhau 1 chút, mọi yếu tố khác ngang nhau, lũy thừa 10 sẽ cho ta 2 con số 1,048,576 và 9,765,625. Đôi lúc 1 khác biệt nhỏ ở xuất phát điểm có thể hoàn toàn do may mắn, được tích lũy qua hàng năm sẽ tạo ra 1 khác biệt đáng kể sau 1 khoảng thời gian (dĩ nhiên mọi yếu tố khác như nhau). Trong khoa học, quy tắc này cũng được biết đến với tên gọi là lợi thế tích lũy (cumulative advantage)

May mắn quan trọng hơn ta nghĩ rất nhiều hoàn toàn khác với tất cả những gì ta cần để thành công trong cuộc sống là may mắn.
Cờ vua hay poker?
Bàn luận về tư duy poker và tư duy cờ vua
Cờ vua là một môn thể thao đối kháng mang tính trí tuệ cao. Có 1 quan điểm phổ biến rằng những người chơi tốt cờ vua sẽ giỏi làm tướng/lãnh đạo trong công ty vì tư duy cờ vua có rất nhiều điểm tương đồng với tư duy chiến lược. Đây là một quan điểm rất hợp lí, hợp lí tới mức chẳng ai thật sự suy nghĩ xem điều này có thật sự đúng hay không?
Bác Daniel Kahneman luôn cảnh báo rằng phải cảnh giác với những câu chuyện có vẻ hợp lí, câu chuyện càng hợp lí với trực giác sống của ta thì sự tự tin vào độ chính xác của nó càng cao, nhưng nó có là chân lí hay không thì là một chuyện khác.

Cờ vua là một môn thể thao có luật riêng của nó, như bao môn thể khác khác. Mỗi người chơi di chuyển quân mình theo lượt, và các quân khác nhau có luật lệ di chuyển của riêng nó (quân tốt không thể di chuyển như quân xe). Nếu bạn suy nghĩ kĩ, tuy số lượng các nước có thể đi cho từng trường hợp cố định là rất lớn (sẽ tăng theo thời gian ván đấu diễn ra) nhưng tuyệt nhiên trong bất kì 1 tình huống cụ thể luôn có 1 lựa chọn tốt nhất. Bạn có thể không đủ trình độ để tìm ra nhưng sự lựa chọn tốt nhất vẫn luôn ở đó. Sự khác biệt trong đẳng cấp là dân pro cảm nhận được những bước đi này trong tích tắc trong khi dân nghiệp dư có khi ngồi suy nghĩ cả ngày cũng không nghĩ ra. Đây là lí do trình độ trong cờ vua gần như quyết định kết quả trận đấu, và bản thân người xem cũng dường như ủng hộ điều này, người có trình độ cao hơn xứng đáng thắng hơn.
Trong cờ vua, đối với người có trình độ cao hơn, trừ khi họ phạm sai lầm, họ sẽ luôn thắng đối thủ yếu hơn. Đây là môn thể thao nếu bạn đưa ra mọi quyết định đúng, bạn không thể thua. Nghe có vẻ là tuyệt vời nhưng đây chính xác là lí do vì sao cờ vua không dạy bạn những kĩ năng quan trọng nhất. Trong cuộc sống, quân tốt có thể đột nhiên di chuyển như quân xe, quân vương không phải là mục tiêu bạn phải giết để thắng mà là quân hậu (không ai nói cho bạn biết điều này, bạn phải trả một cái giá rất đắt để biết), đối thủ của bạn có thể không đợi tới lượt mình mà đi liền 1 lúc 5 lượt và chiếu bí bạn, ....AbC... 123....và xYz.... Sự ổn định bất biến trong cờ vua tạo ra cảm giác an toàn và dễ đoán khi kĩ năng quyết định tất cả.
Trong cờ vua của cuộc sống, nếu bạn đang thắng thế, đối thủ bạn có quyền lật bàn và rời cuộc chơi như không có chuyện gì cả
Không công bằng? Chính xác, và đó là bài học đầu tiên của poker. Trong poker, bạn có thể đưa ra mọi quyết định đúng, nhưng bạn vẫn có thể thua vì thằng kia ăn may, và bạn không thể làm gì khác ngoài việc chấp nhận. Cờ vua là môi trường dễ dự đoán, ở nơi mà may mắn hầu như không tồn tại thì kĩ năng quyết định tất cả, người có trình độ tốt hơn gần như chắc chắn sẽ giành chiến thắng. Tuy nhiên, bài học về tính công bằng trong cờ vua là bài học sai trong cuộc sống!
Poker cũng có thể được xem là một môn thể thao trí tuệ với luật lệ của riêng nó, nhưng về bản chất poker vẫn là trò cờ bạc (nhưng không hoàn toàn đỏ đen như roulette). Người viết sẽ không giải thích quy luật và chiến thuật của poker, nhưng poker giống với cờ vua là trong bất kì 1 tình huống cố định luôn có lựa chọn đúng nhất (call, fold, hay all-in) và người chơi có kĩ năng cao sẽ luôn nhận thức được lựa chọn này. Vấn đề làm cho poker là môn gây stress khá cao là bạn có thể đưa ra mọi quyết định đúng nhưng thần may mắn lại mỉm cười với đối thủ.
Dân chơi poker chuyên nghiệp có thể xem là dân pro về xác xuất, đặc biệt là kĩ năng Bayesian Updating. Với mỗi thông tin đối phương đưa ra, có thể đến từ cách họ nhìn chip, cách họ đưa ra quyết định, thậm chí những cuộc nói chuyện tưởng chừng vô thương vô phạt, dân poker pro sẽ luôn cập nhật tỷ lệ phần trăm chiến thắng và đưa ra quyết định phù hợp, những người chơi giàu kinh nghiệm thường sẽ có khả năng đánh hơi nhạy bén xác xuất đang có lợi cho họ hay không?

Poker là môi trường hoàn hảo để cẩm nhận trực quan về cách xác xuất vận hành. Mọi thứ có thể diễn ra sẽ xảy ra nếu như tập mẫu thử rất lớn. Một người nắm giữ 90% tỷ lệ nếu có thua thì cũng không có gì lạ vì 90% chiến thắng cũng có nghĩa là 10% thua cuộc. Và khi bạn đã chơi poker đủ nhiều (tập mẫu thử đủ lớn), không có tình huống gì có thể làm bạn ngạc nhiên.
Poker đã dạy cho người viết 3 bài học quan trọng:
1. Sự chấp nhận về tính bất định là bài học quan trọng nhất trong poker.
2. Bài học thứ hai là dù đôi lúc cuộc sống khốn nạn, về lâu dài những người đưa ra quyết định đúng thì chắc chắn sẽ lấy tiền từ những người đưa ra quyết định thiếu chính xác. May mắn có thể là 1 yếu tố quan trọng nhưng thần may mắn lại không thích mỉm cười liên tục.
3. Bài học thứ 3 là để đạt được bài học thứ 2, quyết định dựa theo Bayesian Updating là bắt buộc.
Cuộc sống giống với poker nhiều hơn là giống cờ vua
Tại sao Nassim Taleb không thích "mặt trời mọc" của Nate Silver?
Vấn đề của Bayesian Updating
Nassim Tableb là một tác giả nổi tiếng luôn gây tranh cãi trong cộng đồng tri thức. Ông là chuyên gia về rủi ro, là người đã phổ biến hóa cụm tù "Thiên Nga Đen", một thuật ngữ dùng để chỉ những sự kiên tương lai không thể dự đoán, rất hiểm xảy ra, và có ảnh hưởng mang tính thay đổi toàn cầu. Khi đọc lại cuốn "Thiên Nga Đen" được xuất bản năm 2007, người viết nhận ra 1 điều mà lần đầu đọc không nhận thấy, Taleb đã mô tả một sự kiện Thiên Nga Đen rất giống với khủng hoảng tài chính 2008-2009. Ta nên nhớ là cuốn sách Thiên Nga Đen được xuất bản năm 2007, 1 năm trước sự kiện sụp đổ tài chính toàn cầu. Dưới đây là 1 đoạn nguyên văn được viết bởi tác giả Taleb
Chúng ta chưa từng phải sống trong 1 thời đại với mối họa của sự sụp đổ toàn cầu như hiện nay. Các tổ chức tài chính hợp nhất với nhau để trở thành những ngân hàng lớn và quyền lực. Do đó tất cả các ngân hàng quan trọng ngày nay đều có kết nối với nhau. Hệ sinh thái tài chính đang dần biến thành 1 môi trường quan liêu khổng lồ, liên kết chặt chẽ với nhau. Khi 1 ngân hàng phá sản, tất cả ngân hàng đều cùng phá sản.
Taleb không hề dự đoán về khủng hoảng tài chính một năm sau khi xuất bản cuốn sách của mình, ông chỉ nói rằng với môi trường tài chính hiện nay nếu như thảm họa có xảy ra thì hậu quả sẽ cực kì nghiêm trọng do tính chất liên kết mật thiết giữa các nút quan trọng trong hệ thống tài chính toàn cầu. Thiên Nga Đen không thể dự đoán, nhưng với môi trường tài chính hiện tại không hề có hệ thống phòng thủ vững chắc, Taleb cho rằng ngành tài chính ngân hàng sẽ phá sản hàng loạt nếu Thiên Nga Đen gõ cửa ghé thăm. Một năm sau đó, 2008, khủng hoảng tài chính xảy ra gần như làm suy sụp toàn bộ nền kinh tế thế giới. Khủng hoảng tài chính toàn cầu 2008-2009 là một Thiên Nga Đen.

Trong cuốn sách của mình, Taleb đã miêu tả chi tiết các hạn chế của việc dùng các quan sát thực nghiệm trong quá khứ để củng cố lí thuyết cá nhân. Taleb thực sự có vấn đề với Bayesian Updating. Charlie Munger, đồng sự của Warren Buffet từng nói "Tôi chưa bao giờ cho phép bản thân giữ một quan điểm trừ khi tôi có thể sử dụng quan điểm của đối thủ tốt hơn cả chính họ", ở phần này người viết sẽ phản biện lại bài Bayesian Updating của chính mình đã viết trước đó, và sẽ nêu ra những sai lầm có thể mắc phải khi sử dụng quá trình tư duy này.
"I never allow myself to have an opinion on anything that I dont know the other side's argument better than they do" Charlie Munger
Nate Silver, một nhà dự đoán chính trị nổi tiếng của Mỹ, trong quyển sách Signal and noise đã đưa ra một ví dụ để diễn tả quá trình tư duy Bayesian Updating nổi tiếng
Hãy giả định rằng có một người đàn ông vừa được ban cho sự sống trong 1 thế giới mà anh ta không hề có 1 tí kiến thức nào về nó. Lần đầu tiên trong đời anh ta nhìn thấy mặt trời mọc, anh ta đã gào rú hoảng loạn và tìm chỗ trốn khỏi ánh nắng của nó. Anh không biết rằng hiện tượng "mặt trời mọc" này là bình thường hay chỉ là một sự điên loạn trong thế giới. Tuy nhiên, ngày qua ngày khi anh nhìn thấy mặt trời mọc thì anh càng chắc chắn đây là hiện tượng bất biến chứ không hề ngẫu nhiên. Ngày đầu tiên khi anh nhìn thấy mặt trời mọc, anh không hề chắc chắn rằng liệu ngày mai mặt trời sẽ lại tiếp tục được nhìn thấy. Tuy nhiên, con số xác suất này sẽ càng tăng dần (nhưng sẽ không bao giờ đạt đến 100%) với số ngày trong tương lai anh tiếp tục nhìn thấy mặt trời mọc.
Đây là một quá trình tư duy rất tốt, và đặc biệt hiệu quả trong poker, nhưng có những hạn chế không thể tránh khỏi. Nếu như người đàn ông trong ví dụ ngày qua ngày đều nhìn thấy mặt trời mọc, những thông tin trên sẽ ngày càng củng cố giả định "Mặt trời mọc là hiện tượng bình thường".
Nhưng nếu có một giả định khác là "Mặt trời chỉ xuất hiện trong số ngày nhất định và sau đó sẽ không mọc lên nữa" (nói theo khoa học là mặt trời sẽ đốt hết năng lượng và trở thành sao lùn trắng), thì sự quan sát "mặt trời mọc hàng ngày" cũng sẽ củng cố giả định này. Ngày qua ngày mặt trời xuất hiện sẽ đưa thế giới đến gần với kết cục một ngày nào đó mặt trời sẽ không còn chiếu sáng nữa (khi nó đốt hết năng lượng).
Đây là lí do Taleb đã phổ biến hóa khái niệm "Thiên Nga Đen". Giả sử ta có khẳng định rằng "Mọi thiên nga đều trắng", khi quan sát trong thực tế ta phát hiện có 1,000 hay 10,000 thiên nga trắng đều không quan trọng. Tất cả những gì ta cần là 1 Thiên Nga Đen để phá bỏ hoàn toàn khẳng định trên. Ta có quan sát được 1 vạn hay 1 triệu ngày mặt trời mọc lên cũng chỉ tạm thời chứng minh khẳng định "Mặt trời mọc là hiện tượng bất biến". Một ngày mặt trời không còn chiếu sáng là đủ để hoàn toàn bác bỏ khẳng định trên.
Bayesian Updating không phù hợp trong một thế giới tồn tại Thiên Nga Đen, hay còn gọi là môi trường bị thống trị bởi hàm mũ. Lí do Bayesian Updating hoạt động rất hiệu quả trong poker là vì poker là một thế giới không có Thiên Nga Đen. Một bộ bài chỉ có 52 lá, do đó xác xuất luôn cố định trong mọi trường hợp. Trong tài chính, xác xuất trong poker được gọi là rủi ro (có thể biết) trong khi xác xuất trong thế giới của Thiên Nga Đen là bất định (không thể biết). Do bộ bài chỉ có 52 lá, bạn không phải lo sợ trường hợp đột nhiên có thêm 10 lá bài xuất hiện trong bộ bài; bạn không phải lo sợ khi bạn đã giữ 2 lá Ace trong tay, đối phương có thể giữ 3 lá Ace, có rất nhiều sự chắc chắn trong cách xác xuất phân bổ.
Cách tốt nhất để sử dụng Bayesian Updating một cách an toàn là bạn phải chắc chắn rằng thông tin củng cố (hay phủ nhận) chỉ có thể phù hợp với duy nhất một giả thuyết. Lấy ví dụ trong bài Bayesian Updating của mình, bạn dùng các thông tin để củng cố hay phủ nhận giả thuyết "Crush cũng thích mình". Nhưng nếu thế thì bạn phải chắc chắn các thông tin bạn dùng, từ việc crush đi xem phim với mình, hay crush đi xem chơi, đi ăn, nhắn tin etc; crush chỉ làm những điều trên với người crush thích. Nếu crush cũng làm những điều đó với bạn thân hay anh trai mưa, thông tin bạn dùng để chứng minh giả thuyết "Crush cũng thích mình" cũng sẽ bị trùng lặp với các giả thuyết "Crush xem mình như bạn thân" hay "Crush xem mình như anh trai mua".
Những thông tin gì chỉ phù hợp duy nhất với giả thuyết "Crush cũng thích mình"?
1. Crush hun bạn trên môi
2. Crush nắm tay bạn và nhìn bạn với ánh mắt "dâm tình"
3. Crush nói "Làm bạn/anh trai/em gái nuôi nha? "
4. Crush nói "Em thích anh/Anh thích em"
5. Crush tỏ vẻ chiếm hữu/ghen lồng lộn khi bạn gần đối tượng khác giới
6. Crush làm mai cho bạn với bạn thân.
7. Etc

Dành cho những bạn yêu thích đồ thị, đây là ví dụ mình dùng để chứng minh luận điểm trên. Giả sử ta có 1 đồ thị đường thẳng (đồ thị số học)

Nếu bạn tiếp tục kéo dài đường thẳng (dùng thông tin quá khứ để dự đoán tương lai), cái bạn có vẫn sẽ là đường thẳng thuộc riêng về số học. Nhưng mà khoan đã

Nếu bạn phóng đủ to đoạn đường đầu tiên của đồ thị hàm mũ, nó trông cũng rất giống với đường thẳng đấy. Bây giờ giả sử đường thẳng số học ở đồ thị đầu tiên thực chất là thuộc hàm mũ, nếu ta lại dùng thông tin quá khứ để kết luận tương lai, ta sẽ có 1 đường đi lên mãi mãi thuộc riêng về hãm mũ, nhưng mà
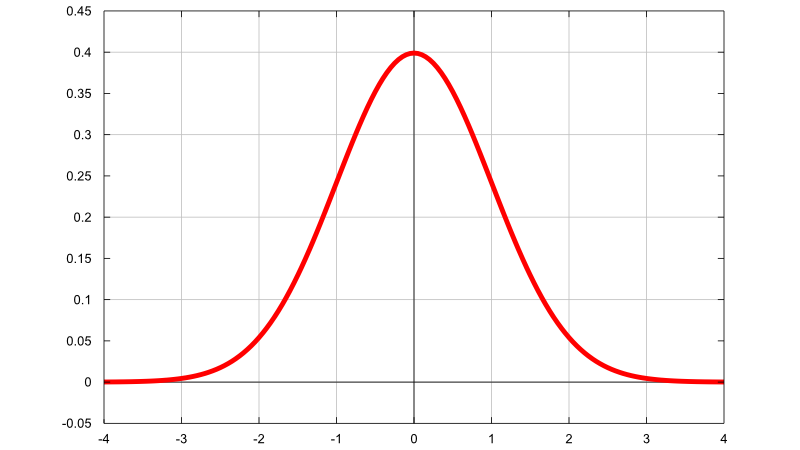
Bạn có thấy gì quen thuộc không? Nửa bên trái của đồ thị hình chuông nhìn rất giống với hàm mũ đấy!
Đây là lí do vì sao đồ thị hàm mũ bị giấu kín? Vì sao Bayesian Updating lại có hạn chế rất lớn trong thế giới Thiên Nga Đen? Vì sao nếu gái chỉ nhắn tin và đi chơi thì cũng không thể chắc chắn rằng em ấy đổ bạn? Những thông tin bạn dùng để củng cố hay phủ nhận giả thuyết cá nhân cũng có thể dùng để phủ nhận hay củng cố giả thuyết khác.
Thế giới của Thiên Nga Đen không thuộc về rủi ro (risk) mà là bất định (uncertainty)
Vậy giờ tính sao?
Bản đồ và địa hình là hai thứ rất khác nhau
Bản đồ của thế giới không phải là thế giới. Cho dù bản đồ tốt nhất cũng không hoàn hảo. Bản đồ là sự đơn giản hóa của thế giới, nó cần thiết khi ta cần một công cụ để nhìn vào thế giới mà không bị nổ não bởi sự phức tạp của nó, nhưng cũng vì thế mà đừng bao giờ quên đi sự phức tạp luôn bị lược bỏ trong bản đồ.
"Bản đồ không phải là địa hình" Alfred Korzybski
Bản đồ là cần thiết để lưu giữ tất cả những chi tiết quan trọng của địa hình trên 1 tấm giấy hữu hạn thông qua việc đơn giản hóa thông tin, nhưng đi cùng luôn là sự lược bỏ những thông tin khác. Chính sự đơn giản hóa làm cho bản đồ không hoàn hảo, nhưng nếu để bản đồ chứa đầy đủ thông tin của địa hình, nó sẽ mất đi tính hữu dụng. Bản đồ không phải là địa hình, khi ta cầm bản đồ trên tay (các quy luật cuộc sống, lí thuyết khoa học, trực giác) ta luôn phải nhớ rằng nó chỉ là sự đơn giản hóa của địa hình. Do đó nó luôn có điểm yếu!

Điều quan trọng là ta phải xác định vành đai bản đồ hoạt động hiệu quả, và khi nào thì bản đồ không còn chính xác. Ví dụ như Bayesian Updating rất hiệu quả trong việc cập nhật niềm tin trong 1 thế giới không có Thiên Nga Đen hoặc 1 thế giới nếu bạn sai về Thiên Nga Đen thì hậu quả cũng không nghiêm trọng. Tuy nhiên, trong 1 thế giới khi mà tần suất xảy ra Thiên Nga Đen quá hiếm, sự ổn định có thể gây ra ảo giác an toàn, nhưng sự thật là Thiên Nga Đen vẫn đang chờ cơ hội để xuất hiện phá bỏ hoàn toàn niềm tin mà ta đang có. Rất nhiều chuyên gia tài chính tin rằng thị trường nhà đất không thể sụp đổ vì nó chưa bao giờ xảy ra trong quá khứ đều phải hứng chịu thịnh nộ của Thiên Nga Đen 2008-2009.
Thế giới mà ta đang sống bị ảnh hưởng rất lớn bởi các sự kiện Thiên Nga Đen, đồ thị hãm mũ là minh chứng cho điều này. Những điều có thể dự đoán thường (phần lớn các sự kiện xảy ra xung quanh thế giới) là phù du không quan trọng, chính những điều không thể dự đoán, hoặc được cho là không thể xảy ra (tập hợp nhỏ những sự kiện then chốt), chính là những sự kiện sẽ thay đổi toàn bộ thế giới. Internet (Thiên Nga Đen tích cực) và khủng hoảng tài chính 2008-2009 (Thiên Nga Đen tiêu cực) là những minh chứng rõ nét nhất.
Điểm hạn chế lớn nhất của Bayesian Updating cũng chính là quy tắc bất di bất dịch trong khoa học. Một lí thuyết không bao giờ được cho là sẽ đúng mãi mãi, nó chỉ tạm thời đúng cho tới khi kiến thức mới được phát hiện bác bỏ lí thuyết cũ. Crush của bạn có nhắn tin, đi ăn với bạn bao nhiêu ngày trong quá khứ cũng chỉ tạm thời chứng minh "Crush có tình cảm với bạn", tất cả những gì thế giới cần để phủ định điều trên là 1 sự kiện ngẫu nhiên đập tan niềm tin của bạn. Trong 1 buổi hẹn với crush, 1 thanh niên/thiếu nữ lạ mặt bước vào và crush giới thiệu "Đây là bạn trai/bạn gái của mình, hai người làm quen nha". Nghe như sét đánh nganh tai!
Tuy nhiên, nếu đọc giả có hỏi thì mình vẫn sẽ dùng Bayesian Updating trong việc phân tích khả năng đối phương có tình cảm với mình. Vì sao? Vì nếu có sai thì cũng chả có gì kinh khủng cả, tình xuống xấu nhất là bạn mất đi một mối quan hệ bạn bè thôi. Trong một môi trường không có Thiên Nga Đen, hãy xử dụng Bayesian Updating bất cứ khi nào có thể. Tuy bạn luôn có thể sai nhưng có một con số cụ thể luôn tốt hơn là không có, và nếu bạn sai thì hậu quả cũng không lớn. Nhưng trong 1 hệ thống phức tạp có nhiều nút liên kết chặt chẽ với nhau (hệ thống tài chính, mạng xã hội, truyền thông, etc), 1 tính toán sai lầm có thể đưa ra những hệ lụy không thể tưởng tượng, đặc biệt là các sự kiện Thiên Nga Đen.
Thật sự đây là một chủ đề rất phức tạp, và thật sự rất khó khăn để diễn đạt hết trong 1 bài blog. Người viết cũng không am hiểu như bác Taleb, người đã dành gần cả đời của mình để nghiên cứu về xác xuất, rủi ro và bất định. Nhưng hi vọng bài blog này có ích cho đọc giả

Quan điểm - Tranh luận
/quan-diem-tranh-luan
Bài viết nổi bật khác
- Hot nhất
- Mới nhất