London, nơi diễn ra kỳ thi Olympic Toán năm 1979.
London, nơi diễn ra kỳ thi Olympic Toán năm 1979. |
Ảnh bởi
Charles Postiaux
trên
Unsplash
Toán học ở một trình độ nhất định sẽ trở thành nghệ thuật.

Trong lịch sử toán học Việt Nam, có những cá nhân đã ghi dấu ấn không chỉ bằng tài năng, mà còn bằng cách họ giải những bài toán phức tạp bằng những lời giải đơn giản nhưng sâu sắc.
Một trong số đó là thầy Lê Bá Khánh Trình – người đã để lại dấu ấn đậm nét tại kỳ thi Olympic Toán học Quốc tế (IMO) năm 1979 ở London, vương quốc Anh.
Tại kỳ thi này, với tài năng và sự nhạy bén, chàng học sinh Quốc học Huế đã giành giải đặc biệt cho lời giải xuất sắc và độc đáo bên cạnh Huy chương vàng với số điểm tuyệt đối 40/40.
Nhận thấy lời giải này có thể được hiểu và cảm nhận bởi tất cả các bạn trẻ, những học sinh yêu toán với kiến thức cơ bản về hình học phổ thông, tôi xin chia sẻ với các bạn bài toán và lời giải mà thầy đã dành được giải thưởng và giải thích vì sao lời giải này lại được đánh giá cao như vậy.

Đề bài

Cho hai đường tròn tâm O1, O2 trên cùng một mặt phẳng cắt nhau. Gọi A là một trong các điểm giao nhau. Xuất phát đồng thời từ A, hai điểm M1, M2 di chuyển với vận tốc không đổi, mỗi điểm di chuyển dọc theo đường tròn của mình theo cùng một chiều. Hai điểm này trở lại A đồng thời sau một vòng quay. Chứng minh rằng tồn tại một điểm cố định P trên mặt phẳng sao cho hai điểm M1, M2 luôn cách đều P.
Bạn nắm được đề bài rồi chứ 😅? Bạn có ý tưởng giải bài toán này như thế nào không? 
Đáp án ban đầu của nhóm ra đề (người Liên Xô) phải dùng một số định lý, tính chất hình học và lượng giác không quen thuộc. Hãy xem thử thầy Lê Bá Khánh Trình đã giải bài toán này thế nào nhé.

Lời giải

(có chỉnh sửa để bạn đọc dễ hiểu hơn)
Gọi B là giao điểm còn lại giữa hai đường tròn. Gọi C, D lần lượt là điểm đối xứng của B qua tâm O1 và O2. Ta sẽ chứng minh trung điểm của CD là điểm P cần tìm. (Amazing!)
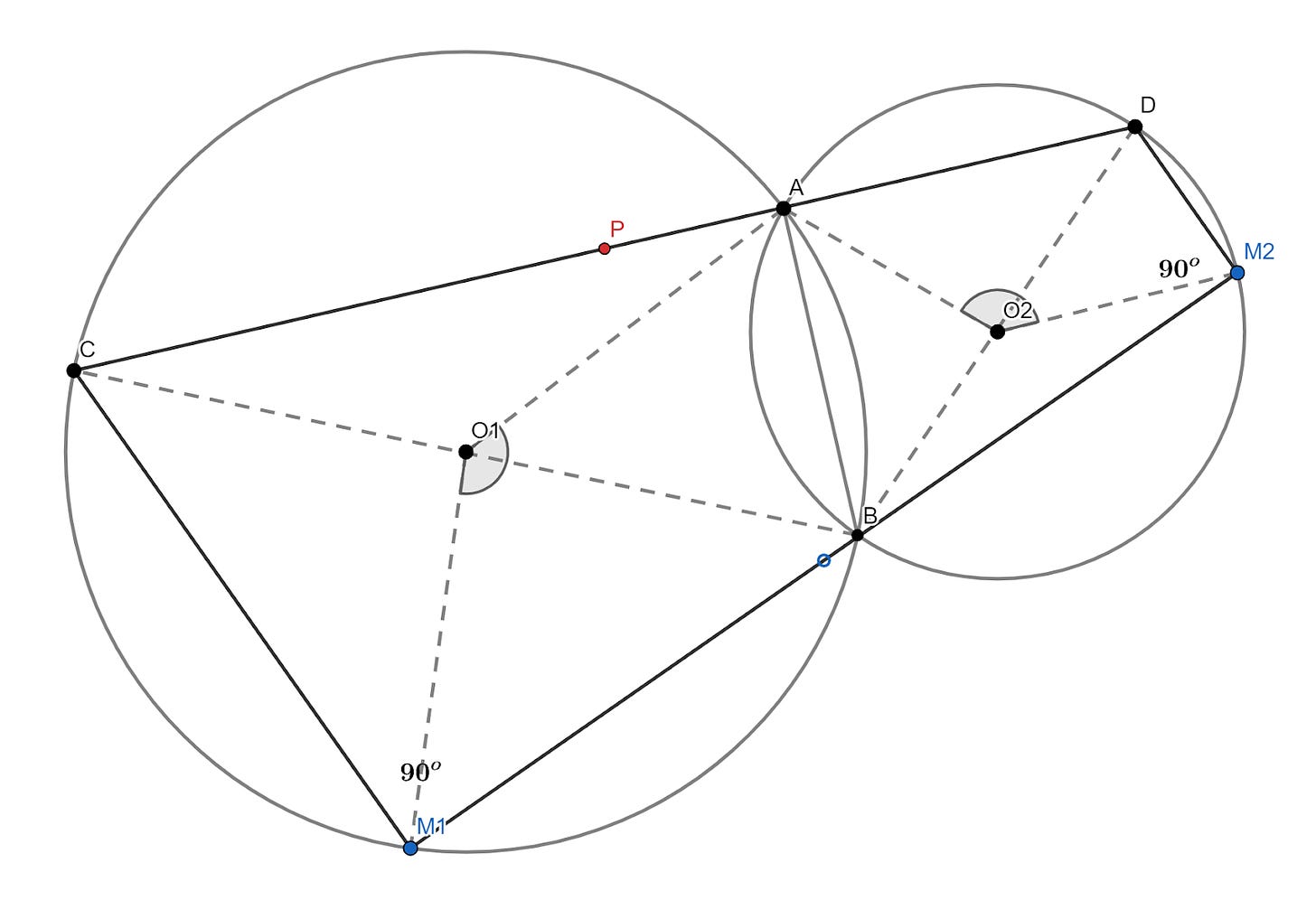
Hình minh họa lời giải bài toán. (mình vẽ bằng Geogebra Geometry)
Hình minh họa lời giải bài toán. (mình vẽ bằng Geogebra Geometry)
Thật vậy!
Xem hai đường tròn như hai chiếc đồng hồ có điểm thời gian xuất phát từ A; hai bán kính O1M1, O2M2 quay như hai kim đồng hồ.
Vì sau một vòng hai điểm trở về A cùng một lúc, nên tại một thời điểm bất kỳ, hai góc AO1M1, AO2M2 luôn bằng nhau bởi chúng thể hiện thời gian đã di chuyển (hình vẽ giống như góc của phút thứ 23!).
Trong đường tròn tâm O1, góc ở tâm AO1M1 lớn gấp đôi góc nội tiếp ACM1. Tương tự, góc AO2M2 lớn gấp đôi góc ABM2. Suy ra góc ACM1 bằng góc ABM2.
Tính chất trên của góc ở tâm cũng dẫn đến hai góc nội tiếp đối nhau ACM1, ABM1 có tổng bằng 180 độ. Điều này cho ta hai góc ABM1 và ABM2 có tổng bằng 180 độ. Tức là ba điểm M1, B, M2 thẳng hàng.
Ta có BC, BD là các đường kính nên BM1C và BM2D là các góc vuông (bạn cũng có thể dùng tính chất góc ở tâm để chứng minh tính chất này luôn). Vậy M1M2DC là một hình thang vuông tại M1 và M2. Nên đường trung bình đi qua P của hình thang này cũng vuông góc với M1M2. 
Điều đó dẫn đến tam giác PM1M2 có đường cao cũng là trung tuyến nên nó là một tam giác cân tại P. Suy ra PM1 bằng PM2. Mặt khác, B, C, D là các điểm cố định nên P cũng cố định.
Vậy P là điểm cần tìm🥰.

Vì sao lời giải này được trao giải đặc biệt?

Theo tôi lời giải của thầy Lê Bá Khánh Trình đặc biệt xuất sắc bởi sự kết hợp hài hòa giữa ba yếu tố: đơn giản, trực quan, và sâu sắc.
- Đơn giản: Thay vì sử dụng những công cụ toán học phức tạp như lượng giác hay các tính chất hình học phức tạp, thầy đã chọn cách tiếp cận bằng những kiến thức hình học sơ cấp mà học sinh phổ thông lớp 9 cũng có thể hiểu được. Chính sự đơn giản này khiến lời giải trở nên gần gũi, không chỉ với các nhà toán học, ban giám khảo cuộc thi, mà còn với những người yêu toán ở mọi trình độ (trên lớp 9😅).
- Trực quan: Lời giải của thầy không chỉ dễ hiểu mà còn rất trực quan. Thầy sử dụng những hình ảnh quen thuộc như góc ở tâm, góc nội tiếp đường tròn, hình thang vuông và tam giác cân để giải thích vấn đề. Những yếu tố này giúp người đọc dễ dàng hình dung và theo dõi từng bước lập luận một cách mạch lạc. Trực quan chính là yếu tố khiến lời giải trở nên sinh động và dễ nhớ.
- Sâu sắc: Mặc dù đơn giản và trực quan, lời giải của thầy không hề thiếu chiều sâu. Thầy đã tinh tế nhận ra rằng, sự đối xứng, song song, vuông góc và tính chất của các góc trong hình học cơ bản có thể dẫn đến một kết luận bất ngờ và độc đáo. Việc chỉ ra điểm P cần tìm chính là trung điểm của đoạn thẳng CD là một khám phá sâu sắc về cấu trúc hình học của bài toán.
Công nương xứ Gloucester (người Đan Mạch), trao giải đặc biệt cho Lê Bá Khánh Trình. (ảnh của chính thầy Trình lưu)
Công nương xứ Gloucester (người Đan Mạch), trao giải đặc biệt cho Lê Bá Khánh Trình. (ảnh của chính thầy Trình lưu)
Chính sự hội tụ của ba yếu tố này – đơn giản, trực quan, và sâu sắc – đã khiến lời giải của thầy Lê Bá Khánh Trình trở nên đặc biệt và được trao giải thưởng cao quý tại kỳ thi IMO năm 1979.
Đối với tôi lời giải này không chỉ mang lại một đáp án đẹp mà còn truyền tải một triết lý toán học:
Đôi khi, cách tiếp cận đơn giản nhất lại là cách hiệu quả và ấn tượng nhất.
Một bài toán có thể có nhiều cách giải. Đặc biệt là bài toán này. Thật ra đây là một bài toán không khó đối với các thí sinh năm ấy. Hầu hết thí sinh các nước đều giải được trọn vẹn bài hình học này. Cả bốn thí sinh của Việt Nam đều giải được. Nhưng lời giải của thầy Trình vượt qua tất cả các thí sinh khác để giành được giải thưởng💪.

Vì sao Lê Bá Khánh Trình tìm được lời giải ấy?

Ngay từ khi còn là học sinh, Lê Bá Khánh Trình đã nổi bật với tài năng xuất sắc trong môn hình học. Khả năng nhạy bén và sự tinh tế trong việc nhận diện các yếu tố hình học đã giúp thầy tìm ra lời giải độc đáo cho bài toán này.
Với nền tảng vững chắc ấy, sau này thầy được giao trọng trách giảng dạy và bồi dưỡng môn chuyên về hình học và tổ hợp cho đội tuyển Toán Trường Phổ Thông Năng Khiếu TP.HCM chúng tôi. Thầy còn thường được giao nhiệm vụ dẫn dắt đội tuyển Việt Nam đi dự các kỳ Olympic Toán quốc tế.
Thầy Trình trở lại Anh năm 2024, lần này là Phó Đoàn của Đội tuyển Olympic Toán Việt Nam. (ảnh: Vietnamnet)
Thầy Trình trở lại Anh năm 2024, lần này là Phó Đoàn của Đội tuyển Olympic Toán Việt Nam. (ảnh: Vietnamnet)
Dù không nằm trong đội tuyển toán, những giờ học hình học không gian với thầy tại Trường PTNK đã giúp tôi không chỉ nắm vững kiến thức, mà còn học được cách tiếp cận vấn đề một cách đơn giản và sáng tạo.
Phong cách giảng dạy của thầy cho tôi nhận ra rằng, đôi khi, sự tinh tế và giản dị trong tư duy chính là chìa khóa để giải quyết những bài toán khó khăn nhất.
Thầy có khả năng đặc biệt trong việc đơn giản hóa các vấn đề phức tạp. Thực tế, trong buổi thi năm ấy, lời giải ban đầu của thầy cũng khá phức tạp, nhưng thầy không chấp nhận. Gần cuối giờ thầy đã nhận ra có thể giải bài toán bằng những công cụ hình học sơ cấp đơn giản hơn. Thầy đã chọn cách giải đơn giản đó, làm cho lời giải trở nên dễ hiểu và gọn gàng, không cần sử dụng những công thức hay kiến thức toán học phức tạp.
Phong cách giải quyết vấn đề này không chỉ áp dụng cho bài toán tại IMO 1979 mà còn là dấu ấn đặc trưng trong cách giải quyết vấn đề của thầy và trong con người thầy. Chính sự giản dị và sáng tạo trong cách tiếp cận toán học và trong cuộc sống đã giúp thầy nổi bật và nhận được sự kính trọng từ cộng đồng toán học😍.

Lời kết 

Lời giải của thầy Lê Bá Khánh Trình tại kỳ thi IMO 1979 không chỉ là một thành tựu cá nhân xuất sắc, mà còn là biểu tượng của sự sáng tạo và sự đơn giản trong toán học – những yếu tố đã góp phần làm rạng danh toán học Việt Nam trên trường quốc tế.
Lời giải ấy cho thấy rằng, trong toán học, không phải lúc nào sự phức tạp cũng đồng nghĩa với sự vượt trội; đôi khi, những giải pháp đơn giản, trực quan mới là những giải pháp đẹp và hiệu quả nhất.
Nhưng trên hết, qua câu chuyện về cậu bé vàng của toán học Việt Nam, tôi muốn nói với các bạn rằng:
Hãy không ngừng khám phá, học hỏi, và tin tưởng vào khả năng của chính mình. Đừng ngần ngại tìm kiếm những cách tiếp cận mới mẻ, những lời giải độc đáo cho các vấn đề bạn gặp phải. Sự sáng tạo và đam mê chính là chìa khóa để bạn vươn tới những đỉnh cao mới trong toán học, và xa hơn nữa là trong mọi lĩnh vực của cuộc sống.
Với niềm đam mê toán học và lòng kiên trì, các bạn hoàn toàn có thể viết tiếp những trang sử vẻ vang cho toán học Việt Nam, như thầy Lê Bá Khánh Trình đã làm trong suốt hành trình của mình💪.

Tái bút

Lời giải và hình vẽ có dựa trên bài viết của tác giả Ngô Hân trong Tuyển tập 5 năm Tạp chí Toán học và Tuổi trẻ từ năm 1991 đến năm 1995.
Để đến được rộng rãi hơn, gần gũi hơn với đọc giả, tôi đã cố gắng viết lại lời giải gốc tránh dùng các ký hiệu toán học; chỉ sử dụng từ ngữ thông thường để diễn đạt. Đặc biệt, dùng đồng hồ để giải thích hai góc bằng nhau là ý của tôi. Mong rằng các bạn hiểu được 😅.
Bài viết này được viết lại từ Self-Discovery, bản tin bằng tiếng Việt của tôi.
Trung Học Phổ Thông Bàn về Giáo dục