[Nhập môn Deep Learning] AutoEncoder và Variational Autoencoder: Lý thuyết về Latent Space và ELBO

Mình thấy thích chuỗi podcast "Làm giàu kiểu cụ Hồ" của team Spiderum quá (Cảm ơn team vì một chuỗi podcast cực kì hay, highly highly recommended)! Đến phần thứ 3: Dĩ bất biến ứng vạn biến thì lại cực kì ấn tượng hơn nữa. Mình thích lịch sử và cũng đã đọc nhiều nhưng có những góc nhìn mà tuổi đời chưa đủ để nghiệm ra được như khách mời Nguyễn Thành Nam. Thế rồi mình tự hỏi trong Deep Learning hiện đại, có thứ gì dạng như vậy: "dĩ bất biến, ứng vạn biến" hay không? Câu trả lời là có rất nhiều. Thế thì có cái gì nên biết ở Nhập Môn hay không? Câu trả lời đó chính là VAE (Encoder-Decoder architecture). Thế là sau khi trở lại lab từ kì nghỉ tết ở nhà, mình đã lọ mọ viết tiếp chuỗi bài viết này mặc dù rất nhiều kì hạn mà giáo giao để renew funding contract sắp đến. Trong suốt lịch sử phát triển của Deep Learning, Encoding là một kỹ thuật hoặc nói đúng hơn là một kiến trúc được ưu chuộng sử dụng trong mọi bài toán. Trong các kiến trúc có Encoder, Variational Autoencoder (VAE) là phổ biến, tối ưu, và được sử dụng hiệu quả nhất. VAE là hậu nhân của AutoEncoder (AE) và Principle Component Analysis (PCA). Tuy nhiên, PCA là một phương pháp khá cổ (thuộc về thời đại Machine Learning tiền Deep Learning). AE và VAE vốn chỉ khác biệt một chút, có thể nói là một phép toán, nhưng VAE lại có thể bước ra một bước để trở thành một kiến trúc hiệu quả vượt trội (tất nhiên là với nhiều sự phát triển thêm sau này). Trong bài viết này, tôi sẽ giới thiệu đến độc giả một giới thiệu ngắn gọn, cơ bản, và thiếu sót về AE và VAE. Chú ý rằng, VAE là một phần của các thành công của rất nhiều mô hình hiện đại, tuy nhiên bài viết này chỉ đề cập khái quát về VAE. Để thực sự đạt được khả năng của các mô hình sinh hiện tại là tập hợp rất nhiều những kỹ thuật, nghiên cứu, phát kiến sau này.

Giới thiệu về AutoEncoder và VAE

AutoEncoder là một mạng nơ-ron học cách nén dữ liệu vào không gian latent và tái tạo lại, thường dùng để giảm chiều. VAE, một phiên bản nâng cao, không chỉ tái tạo mà còn sinh dữ liệu mới bằng cách mô hình hóa không gian latent như một phân phối xác suất, thường là Gaussian.

Tại sao lại cần mã hoá dữ liệu? Các dữ liệu ở các ứng dụng/bài toán hiện đại rất lớn và phức tạp. Để máy tính tính toán trên một bộ dữ liệu lớn với từng điểm dữ liệu lại cũng lớn là quá tốn và không cần thiết nếu ta có thể biểu diễn điểm dữ liệu đó ở một không gian có số chiều nhỏ hơn. Nói cách khác, mã hoá làm giảm số chiều dữ liệu, và thường còn biểu diễn được phân phối của bộ dữ liệu (observed) mà nếu đủ lớn có thể xấp xỉ phân phối thật (true probability).

Tại sao lại cần tái tạo lại dữ liệu? Biểu diễn của dữ liệu ở một không gian xác suất mới không phải là thứ con người có thể hiểu vì nó đơn giản là các vector số. Trong khi đó, mục tiêu cuối cùng của con người là: âm thanh, hình ảnh, video, quyết định, dự đoán, etc. Như vậy, ta cần một bộ giải mã (decoder) để tái tạo lại những dạng dữ liệu mà ta cần. Thế cái gì là đầu vào của bộ giải mã này? Câu trả lời nhảy ra ngay trong đầu chính là đầu ra của Encoder (bộ mã hoá). Thế nhưng, "ứng vạn biến", bất kì một mô hình nào làm việc trên latent space mà Encoder tạo ra đều có thể tạo ra đầu vào cho Decoder. Tức là, việc dùng Encoder đã làm đơn giản hoá (simplify) dữ liệu đầu vào, và máy học sẽ chỉ học trên dữ liệu đã mã hoá thôi để tối ưu hiệu năng, hiệu suất, etc. Mà không phải lo về dữ liệu cuối cùng được yêu cầu vì đã có Decoder lo cho rồi!

Kiến trúc và hàm mất mát

Như đã nhắc nhiều ở các bài trước (như là lảm nhảm), một mô hình Deep Learning thì cần có kiến trúc và hàm mất mát.

Hình 1. Kiến trúc và hàm mất mát MSE của AutoEncoder.

Cả AE và VAE đều có Encoder f(x) sẽ encode dữ liệu đầu vào x thành một vector z đối với AE, và tham số mu, sigma của một phân phối đối vối VAE. Chú ý rằng, đầu ra của f trong AE chỉ đơn giản là một vector. Tuy nhiên, đầu ra của VAE lại chính là một phân phối xác suất (các tham số của hàm PDF), thường được chọn là phân phối chuẩn (pre-defined). Nếu gọi phân phối đó là q(z|x), thì có thể viết dưới dạng toán học như sau:

Hình 2. Phân phối xác suất sinh bởi Encoder của VAE.

Hình 3: Sự khác biệt trong đầu ra của AutoEncoder (phía trên) và Variational AutoEncoder (phía dưới).

Vì sự khác biệt của Encoder mà Decoder sẽ có đầu vào khác nhau giữa AE và VAE. Đối với AE, Encoder sinh ra vector gì thì đầu vào chính là vector đó. Mặc khác, đối với VAE, đầu ra của Encoder là một phân phối xác suất, tuy nhiên ta chỉ cần tái tạo một điểm dữ liệu cho hàm mất mát mà thôi. Vì thế, một vector z được sampling (lấy mẫu) từ không gian xác suất sinh bởi Encoder. (Về mặt coding, reparameterization trick thường được sử dụng để sampling.) Và vector z này được đưa vào trong Decoder để làm đầu vào cho quá trình tái tạo x. Đầu ra của Decoder sẽ được kí hiệu là x'.

Như đã trình bày trước đó, mục tiêu của Encoder là làm giảm số chiều của dữ liệu đầu vào, khiến cho thông tin cô đặc hơn (condense). Tuy nhiên, nhiệm vụ tiên quyết của quá trình nén là không được để mất thông tin. Chính vì thế, chỉ khi Decoder tái tạo lại được dữ liệu đầu vào từ thông tin trong vector z, thì ta mới có thể nói z Encoder đã nén được dữ liệu. (Bạn đọc có thể tìm hiểu thêm về lý thuyết thông tin). Như thế, tác vụ chính ở đây chính là tái tạo lại đúng dữ liệu đầu vào sau quá trình Encode và Decode. Vậy đơn giản, ta có thể hàm Mean Squared Error (MSE) làm hàm mất mát cho quá trình huấn luyện.

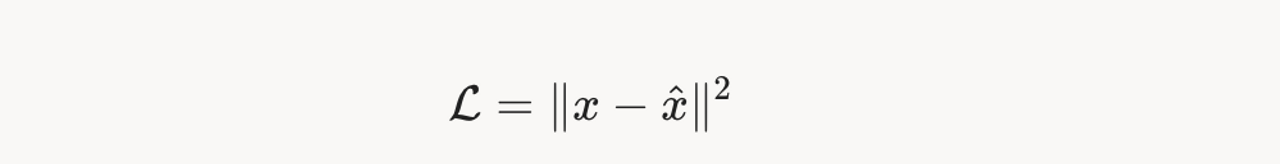
Hình 4: Hàm mất mát MSE, giữa dữ liệu đầu vào và kết quả decoding.

Có một sự thật thú vị là ta có thể chứng minh MSE tương đương với Cross Entropy Loss (một hàm mất mát chuyên cho tái tạo phân phối). Chính vì thế, nếu có lượng dữ liệu đủ lớn thì quá trình huấn luyện mô hình này để tái lại dữ liệu đầu vào thực ra là đang huấn luyện mô hình tái tạo lại chính phân phối xác suất của dữ liệu đầu vào p(x).

Tuy nhiên, VAE có thêm một ràng buộc đó chính là đầu ra của Encoder là phân phối chuẩn. Làm sao để áp đặt ràng buộc này vào mô hình của chúng ta? Câu trả lời đơn giản là biến nó thành một tác vụ cần giải quyết. Vậy thì, thêm ràng buộc này vào hàm loss là được. Chú ý rằng, thực tế ta đang cố gắng tái tạo lại phân phối của dữ liệu đầu vào. Tức là, với bất kì dữ liệu nào mô hình chúng ta sinh ra, xác suất của nó ở trong phân phối p(x) càng lớn càng tốt. Đây chính là objective! Đối với VAE, ta còn biết thêm được một mấu chốt quan trọng đó là latent vector z phải nằm trong một phân phối chuẩn. Nhờ đó, ta có một khai triển cực kì nổi tiếng dẫn đến hàm mất mát tên là ELBO như sau:

Hình 5: Khai triển ELBO. Chú ý ở bước 3, bất đẳng thức Jensen được phát biểu trên tổng, và tích phân chính là một phép tính tổng.

Hình 6. Khai triển ELBO. Hãy chú ý rằng từ đầu đến cuối của khai triển này, ta không hề ràng buộc p(z) phải là một phân phối nào cả. Tuy nhiên, chúng tôi thường hay dùng p(z) là phân phối chuẩn vì nhiều vấn đề cả về lý thuyết cũng như coding. (Bạn đọc có thể tự tìm hiểu về KL-Divergence cũng như lý thuyết thông tin để nắm bắt công dụng của nó, tuy nhiên công thức đã có ở bước thứ 5 rồi)

Hình 7. Ý nghĩa của của các terms trong công thức ở bước thứ 6. Hãy chú ý đến term thứ nhất, nó chính là MSE loss ở AE. Term thứ 2 sẽ đảm bảo rằng latent space sẽ có dạng của một phân phối chuẩn. Như thế là ta đã đảm bảo được objective: (1) tái tạo dữ liệu như AE, (2) đảm bảo p(z) là phân phối chuẩn.

Tại sao VAE vượt trội?

Nếu đọc kĩ phần phía trên, hoặc đơn giản là nhìn vào Hình 3., bạn đọc có thể thấy VAE chỉ khác AE ở chỗ đầu ra của Encoder là một phân phối xác suất thay vì một vector. Chính thay đổi nhỏ bé này đã tạo ra sự vượt trội của VAE so với AE. Nhưng, tại sao? Câu trả lời có thể trả lời như sau:

Bản thân việc encode dữ liệu, compress dữ liệu bởi AE đã có tác dụng lớn trong việc tối ưu quá trình truyền tải dữ liệu rồi. Tuy nhiên, khi làm việc với Deep Learning, truyền phát không phải mục tiêu cuối cùng mà là khả năng "hiểu", "sinh", "xử lý" các dữ liệu. Và AE khó đáp ứng nhu cầu này vì đầu ra của AE không phải là một phân phối biết trước. Ta không rõ hình thù của cái phân phối ấy, lại không chắc rằng phân phối ấy là liên tục (continous) và trơn (smooth) hay không. Thế thì ta khó có thể sinh một data bất kì khi chọn đại một vector nào đó. Nhưng, VAE làm được, vì ta có một phân phối xác suất là đầu ra của Encoder, nên ta có thể chọn vô hạn (theo lý thuyết) số điểm trong phân phối này và đưa vào Decoder. Đây chính là khả năng làm cho mô hình có thể sinh ra hình một chú chó đang bơi trong vũ trụ (một thứ chưa từng có thật).

Và như đã giới thiệu ở phần đầu, nhờ có một phân phối xác suất, mà ta có thể dùng các module khác để làm việc trên phân phối này mà rất tiện lợi. Đây chính là một phần tạo nên thành công của Stable Diffusion, MidJourney, etc.

Kết luận

Hình 8. Tóm tắt tất cả lý thuyết cần nhớ về AE và VAE. Còn về ý tưởng, hi vọng phần bài viết có thể khiến độc giả cảm thấy những thứ này là tự nhiên, hoàn toàn có mục đích chứ không phải tự nhiên ai đó mơ thấy và viết ra.

References

[1] Kingma, D. P., & Welling, M. (2014). Auto-Encoding Variational Bayes. In 2nd International Conference on Learning Representations, ICLR 2014. [2] Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT [3] Press.Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.