Game theory và một số mô hình ứng dụng

John Nash bắt đầu bằng PhD tại Đại học Princeton năm 1948 với một bức thư giới thiệu nói rằng "Đây là một thiên tài toán học". Thật sự vậy, 19 tuổi, dự duy nhất một lớp Kinh tế trong chương trình học Đại học của mình, Nash cho ra đời công trình toán học đầu tiên chỉ sau 14 tháng nghiên cứu, để sau này, năm 1994, ông nhận giải Nobel cho những đóng góp to lớn của mình trong Kinh tế và cụ thể là trong Lý thuyết Trò chơi.

Ngày 16/11/1949, Nash gửi một bản note chỉ dài hơn 1 trang lên Proceedings of the National Academy of Sciences, trong đó ông có giới thiệu về một khái niệm mới trong Lý thuyết Trò chơi, mà sau này nó được biết đến với tên gọi "Cân Bằng Nash". 

Khái niệm này về cơ bản mô tả chiến thuật của một trò chơi cá nhân, chơi bởi những gã khôn ngoan luôn biết tìm cách tốt nhất để tối đa hóa lợi nhuận của mình (making rational choices) dựa trên việc dự đoán về chiến thuật của các đối thủ. Sau đó trò chơi được mô tả là sẽ đạt cân bằng Nash khi tất cả người chơi đã chọn được một chiến thuật tối ưu nhất của mình.

Còn sau đó là phần toán học, Nash chứng minh rằng trong một trò chơi có hữu hạn người chơi và hữu hạn lựa chọn, thì luôn luôn tồn tại ít nhất một cân bằng Nash.

Nghe có vẻ vẫn chung chung quá...Okay, chúng ta sẽ xét một ví dụ cực kì cổ điển của cân bằng Nash:  Prisoner's Dilemma ...nghe gk^e thế nhỉ, thôi gọi là Song đề tù nhân nhé...

Song đề tù nhân đưa ra một tình huống khá là "khoai" (hay còn gọi một cách có học hơn là "tiến thoái lưỡng nan") của hai người tù nhân.

Câu chuyện là thế này: Hai anh chàng xấu số, Khá Bảnh và Khá Đuối, về cơ bản là có tội rồi, nhưng công an thì cần hai anh hợp tác cho lời khai để còn nhanh nhanh kết thúc vụ án. Họ đưa hai anh vào hai phòng tách biệt, chủ yếu là để ngăn mọi sự liên lạc giữa hai người, rồi đưa cho họ 1 offer cực "thơm" như sau.

Nếu anh Bảnh khai mà anh Đuối không khai, thì anh Bảnh được hưởng khoan hồng, thả tự do, trong khi anh Đuối thì bị tù chung thân. Và ngược lại. Còn nếu cả hai anh cùng khai, thì cùng đi tù 2 năm. Còn nếu cùng im lặng, well, công an vẫn sẽ tống cả hai anh vào tù, nhưng 6 tháng thôi.

Dưới góc nhìn của người thứ ba, bạn nghĩ lựa chọn nào sẽ tốt nhất cho cả hai?

Sau đó, chúng ta xét tình huống dưới góc nhìn của từng người tham gia nhé!

Anh Bảnh và anh Đuối về cơ bản thì cũng chả tin tưởng gì nhau lắm, xong lại còn bị cắt đứt liên lạc, nên tình huống bây giờ đưa về trò chơi cá nhân - giống như trong mô tả về cân bằng Nash, với hai người chơi (có thể giả sử là) khôn ngoan là Bảnh và Đuối.

Đặt mình vào vị trí của anh Bảnh, chúng ta thấy có 2 trường hợp, phụ thuộc vào lựa chọn của Đuối : nếu Đuối khai, Bảnh cũng sẽ phải khai (đi tù 2 năm) thay vì im lặng (đi tù chung thân); nếu Đuối im lặng, Bảnh cũng sẽ vẫn khai (được thả tự do) thay vì im lặng (đi tù 6 tháng). Như vậy thì kiểu gì đi nữa, Bảnh cũng sẽ khai.

Đặt vào vị trí của Đuối, tương tự, Đuối cũng sẽ khai.

Cuối cùng, cả hai người đều khai. Ở đây, ta đã đạt được 1 cân bằng Nash, là 1 vector lựa chọn của 2 người (khai, khai) - tức là cả 2 đi tù 2 năm.

Quay lại trò chơi với góc nhìn của một người thứ ba, rõ ràng, việc cả hai người đều im lặng thì sẽ là lựa chọn tốt nhất - tức là cả 2 chỉ đi tù 6 tháng??? Vậy thì tại sao người chơi lại không làm vậy???

Cũng dễ hiểu nè, chủ yếu là vì họ không tin tưởng nhau, và chỉ cố gắng tối đa hóa lợi ích của riêng mình thôi. Và vì vậy, người ta nói, cân bằng Nash chỉ ra rằng: tối đa hóa lợi ích cho từng cá nhân chưa chắc đã là cách tối ưu hóa lợi ích cho một đám đông.

Và sau đây, là một số ứng dụng cổ điển của cân bằng Nash (không chỉ ở trong kinh tế).

Okay, chúng ta sẽ đến với mô hình đầu tiên: Hotelling. 

Bài toán đưa ra như sau: 2 cửa hàng bán kem dự định mở cửa hàng trên 1 con phố đi bộ, ở đó ta giả sử người mua hàng được phân phối đều trên con đường, và ai cũng phải mua 1 và chỉ 1 cây kem. Cả hai cửa hàng cùng bán một loại sản phẩm, y xì nhau từ chất lượng đến giá cả. Thứ mà họ cạnh tranh nhau hiện tại là lượng người mua. Biết rằng, người mua luôn chọn cửa hàng kem gần mình nhất, và nếu 2 cửa hàng cùng đặt trên cùng 1 vị trí (đối diện nhau chẳng hạn), thì thị phần sẽ được chia đôi cho cả hai. Câu hỏi đặt ra là, chiến thuật chọn vị trí của 2 cửa hàng như thế nào để tối đa hóa lượng người mua?

Nhìn vào hình minh họa, ta có thể thấy, cả hai cửa hàng kem luôn có xu hướng tiến gần đến giữa con phố, để tối đa hóa thị phần của mình. Và khi cả hai đã ở chính giữa con phố, chẳng ai muốn chuyển đi nữa cả. Ở đây, ta đạt được 1 cân bằng Nash, và thị phần của mỗi cửa hàng là 50%.

Đứng ở góc nhìn ở người thứ ba, ta đều thấy rằng việc hai cửa hàng nằm cách đều nhau ở 2 bên phố (hình ở giữa, bên trái) là đủ để đem lại thị phần cho họ là 50% - tức là tương đương với cân bằng Nash. Chưa kể, ở vị trí này, người mua chỉ cần đi xa nhất là 1/4 con phố để đến được hàng kem. Trong khi, ở cân bằng Nash, người ở đầu phố phải đi đến 1/2 con phố để mua kem.

Kết luận : Trong cân bằng Nash này, lợi nhuận là tối đa cho cả hai người bán, nhưng lại chưa phải là cân bằng tối ưu cho thị trường chung.

Tiếp theo, ta phân tích một vấn đề thú vị trong quy hoạch giao thông: nghịch lý Braess.

Bài toán được đưa ra dưới dạng giản lược như sau :

Một hệ thống đường, ban đầu chỉ có 2 con đường : Start - A - End và Start - B - End. Trong đó, Start - B và A - End là hai con đường cao tốc có thể chịu được lượng lưu thông khổng lồ, nên thời gian di chuyển trên 2 con đường này là hằng số, 45 phút. Tuy nhiên, 2 cây cầu, Start - A và B - End là nút cổ chai của 2 tuyến đường này, chỉ chịu được lượng lưu thông giới hạn, nên thời gian di chuyển sẽ tỉ lệ thuận với lượng lưu thông : t = T/100, T là lượng phương tiện di chuyển. Tổng lượng xe muốn di chuyển từ Start đến End là 4000.

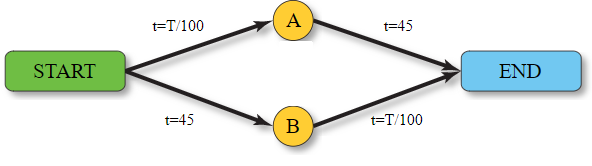
Bài toán ban đầu khá đơn giản. Dễ dàng thấy, lượng xe cộ lưu thông sẽ chia làm đôi, lưu thông trên 2 con đường khác nhau là Start - A - End và Start - B - End. Sẽ không có kẻ khôn ngoan nào đổi ý định, chọn con đường còn lại vì điều đó sẽ kéo theo tăng lượng lưu thông trên cầu, làm chậm thời gian di chuyển đi. Ta có cân bằng Nash. Với thời gian lưu thông của mỗi người là : 2000/100 + 45 = 65 phút.

Bây giờ, người ta muốn cải thiện việc di chuyển trên mạng lưới giao thông này, nên thành phố đã xây dựng thêm một con đường "siêu tốc" A - B. Với công nghệ xây đường vượt trội (có thể  là 1 dạng của Teleport), người ta di chuyển từ A đến B mà không tốn chút thời gian nào, và không phụ thuộc vào lưu lượng xe cộ luôn !!!

Một kẻ ranh ma đang đi trên cây cầu Start - A nghĩ rằng, nếu hắn đi theo con đường Start - A - B - End thì sẽ chỉ mất : 2000/100 + 0 + 2001/100 = 40.01 phút !!! Tiết kiệm được hẳn 25 phút. Nghĩ sao, hắn làm vậy. Rồi không chỉ mình hắn, những người khác đang đi trên cây cầu Start - A cũng làm vậy. Rồi tất cả mọi người đều bỏ con đường A - End mà đi theo lộ trình A - B - End vì : 2000/100 + 0 + 4000/100 = 60, vẫn nhanh hơn là 65 phút !!! Lúc này, người đi theo lộ trình Start - B - End thì tự nhiên bị kéo chậm lại bởi : 45 + 4000/100 = 85 phút !!! Điên tiết, họ lại đồng loạt bỏ con đường Start - B rồi lại đi theo lộ trình Start - A - B - End, bởi vì : 4000/100 + 0 + 4000/100 = 80 phút, vẫn nhanh nhiều so với 85 phút đi theo con đường Start - B - End. Và cuối cùng, tất cả đều đi theo lộ trình Start - A - B - End dù thời gian di chuyển lên tới 80 phút :) Tuy vậy, cũng chẳng ai muốn chọn đi qua Start - B hay A - End, vì đi trên cầu tuy hơi đông nhưng cũng chỉ mất 40 phút, còn đi trên đường cao tốc thì mất những 45 phút cơ :) Ở đây, ta đạt cân bằng Nash, với thời gian di chuyển là 80 phút (?)

Kết luận: Dễ nhận thấy, kể cả khi xây thêm đường A-B, việc mọi người đồng loạt nhất trí không đi trên con đường này thì bài toán quay trở lại ban đầu, và thời gian di chuyển tối ưu chỉ là 65 phút mà thôi. Nhưng vì mọi người đều cố gắng tối ưu hóa việc di chuyển của riêng mình, nên đã kéo dài thời gian lên thành 80 phút, và 2 con đường cao tốc thì bị bỏ không. Một lần nữa, cân bằng Nash cho thấy, đám đông không phải lúc nào cũng khôn ngoan. Và quan trọng hơn, nghịch lý về việc, không phải cứ xây thêm đường thì sẽ giải tỏa được ách tắc giao thông.

Bài toán này còn nhấn mạnh sự cần thiết của việc áp dụng toán học một cách đúng đắn vào quy hoạch đô thị.

Braess's Paradox: Wikipedia, VCP/Havard