Bắt đầu hành trình của chúng ta lên nấc thang trừu tượng, nơi chúng ta bỏ lại đằng sau sự đơn giản khi có thể nhìn thấy mọi công tắc và bánh răng nhưng có được khả năng lắp ráp các hệ thống ngày càng phức tạp
May mắn thay, ngay cả khi chỉ với hai trạng thái điện, chúng tôi có thể đại diện cho thông tin quan trọng, chúng tôi gọi như vậy đại diện Nhị phân (Binary) - Nghĩa đen có nghĩa là "hai trạng thái", giống như cách một chiếc xe đạp có hai bánh hoặc hai chân có hai chân. Nó chính xác những gì bạn cần để đại diện cho các giá trị "true" và "false".
Trong máy tính, trạng thái "bật", khi dòng điện chạy, biểu thị true. Trạng thái "tắt", không có dòng điện chạy qua, đại diện cho false. Chúng ta cũng có thể viết nhị phân là 1 và 0 thay vì true và false- Chúng chỉ là các biểu thức khác nhau của cùng một tín hiệu. Bây giờ thực sự có thể sử dụng bóng bán dẫn cho nhiều thứ hơn là chỉ bật và tắt dòng điện, và cho phép các mức dòng điện khác nhau. Một số máy tính điện tử ban đầu là bậc ba, đó là ba trạng thái và thậm chí là số nhị phân (quinary), sử dụng 5 trạng thái.
Vấn đề là, càng có nhiều trạng thái trung gian, càng khó giữ tất cả chúng - Nếu pin điện thoại thông minh của bạn bắt đầu sắp hết hoặc có tiếng ồn điện do ai đó đang chạy lò vi sóng gần đó, các tín hiệu có thể bị trộn lẫn ... và vấn đề này chỉ trở nên tồi tệ hơn với các bóng bán dẫn thay đổi trạng thái hàng triệu lần mỗi giây! 
Vì vậy, việc đặt hai tín hiệu càng xa nhau càng tốt - chỉ sử dụng "bật và tắt" - cho chúng ta tín hiệu rõ ràng nhất để giảm thiểu những vấn đề này. Một lý do khác khiến máy tính sử dụng hệ nhị phân (Binary) là toàn bộ một nhánh toán học đã tồn tại chỉ xử lý các giá trị đúng và sai. Và nó đã tìm ra tất cả các quy tắc và hoạt động cần thiết để điều khiển chúng. Nó được gọi là Đại số Boolean (Boolean Algebra).

Boolean Algebra
George Boole, mà sau này có tên là Đại số Boolean, là một nhà toán học người Anh tự học vào những năm 1800. Ông quan tâm đến việc đại diện cho các phát biểu lôgic "dưới, hơn và ngoài" (under, over and beyond) cách tiếp cận lôgic học của Aristotle, điều này không có gì đáng ngạc nhiên, dựa trên cơ sở triết học. Cách tiếp cận của Boole cho phép chân lý được chứng minh một cách có hệ thống và chính thức, thông qua các phương trình logic mà ông đã giới thiệu trong cuốn sách đầu tiên của mình, "Phân tích toán học của logic" vào năm 1847.
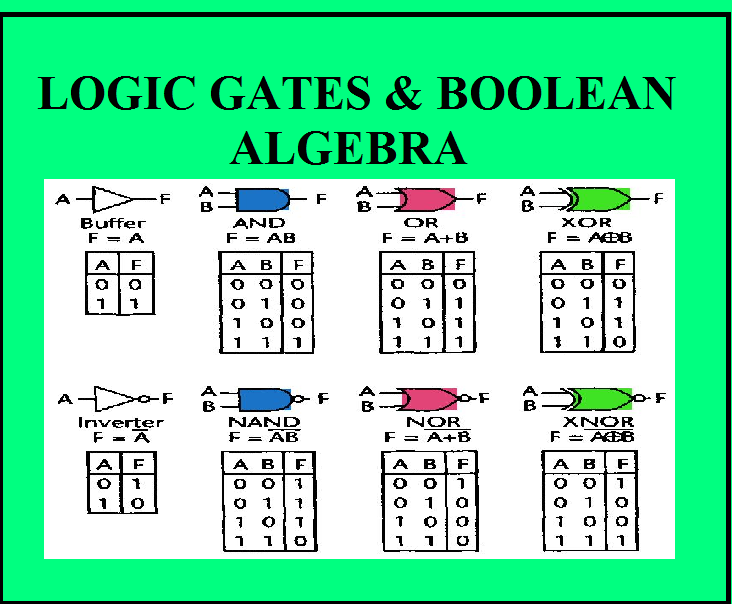
Trong đại số "thông thường" - loại mà bạn có thể đã học ở trường trung học - các giá trị của các biến là số và các phép toán trên những số đó giống như phép cộng và phép nhân. Nhưng trong Đại số Boolean, giá trị của các biến là đúng và sai(True and False) , và các phép toán là logic.

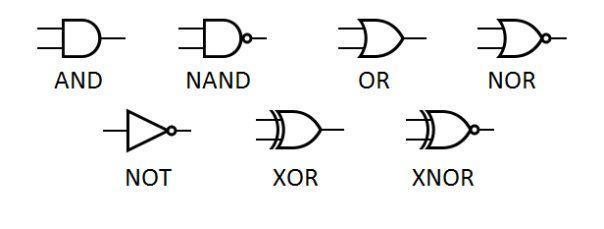
Có ba phép toán cơ bản trong Đại số Boolean: phép toán NOT, AND và OR. và những hoạt động này thực sự hữu ích, vì vậy chúng ta sẽ xem xét từng hoạt động

NOT Gate
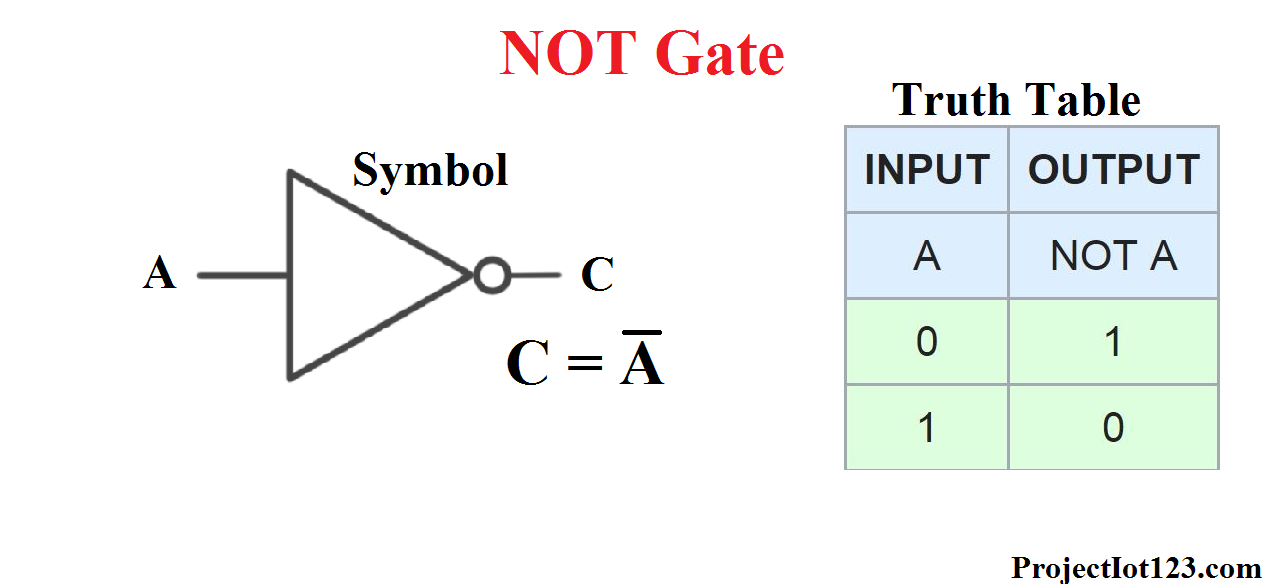
NOT nhận một giá trị boolean duy nhất. hoặc đúng hoặc sai và phủ định nó. Nó chuyển đúng thành sai và sai thành đúng. Chúng ta có thể dễ dàng xây dựng logic boolean từ các bóng bán dẫn. Bạn có thể coi dây điều khiển là đầu vào và dây đến từ điện cực dưới cùng là đầu ra. Vì vậy, với một bóng bán dẫn duy nhất, chúng ta có một đầu vào và một đầu ra. Nếu chúng ta bật đầu vào, đầu ra cũng bật vì dòng điện có thể chạy qua nó. Nếu chúng ta tắt đầu vào, đầu ra cũng tắt và dòng điện không thể đi qua nữa. 
Hoặc trong thuật ngữ boolean, khi đầu vào là đúng, đầu ra là đúng hoặc khi đầu vào là sai, đầu ra là sai. Đây không phải là một mạch quá thú vị vì nó không hoạt động gì cả - đầu vào và đầu ra giống nhau.
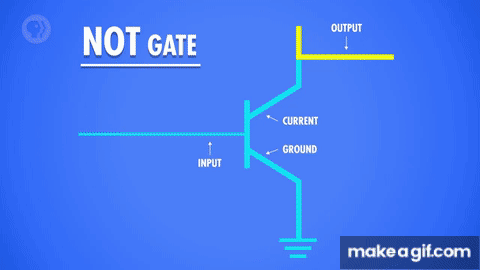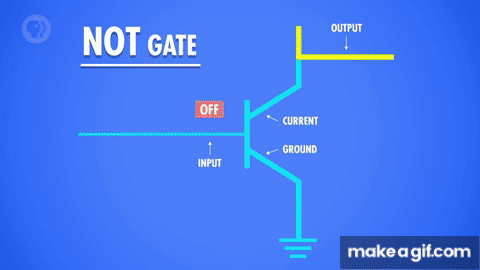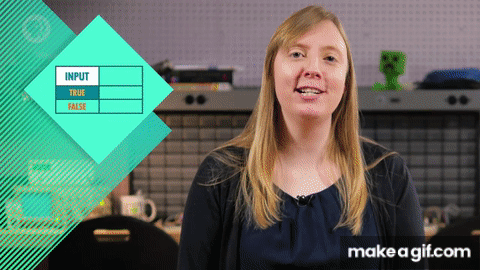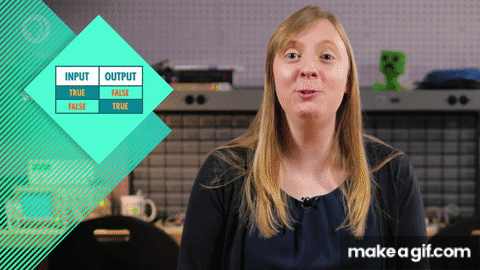
Nhưng chúng ta có thể sửa đổi mạch này một chút để tạo NOT. Thay vì có dây đầu ra ở cuối bóng bán dẫn, chúng ta có thể di chuyển nó trước đó. Nếu chúng ta bật đầu vào trên bóng bán dẫn cho phép dòng điện đi qua nó xuống "Ground" và dây đưa ra sẽ không nhận được dòng điện đó- vì vậy nó sẽ tắt.
Trong trường hợp này nếu đầu vào đang bật, đầu ra tắt, khi chúng ta tắt bóng bán dẫn, tuy nhiên, dòng điện bị ngăn không cho nó chảy xuống đất, do đó, dòng điện chạy qua dây đầu ra.

Vì vậy, đầu vào sẽ tắt và đầu ra sẽ bật. Và điều này phù hợp với bảng logic của chúng ta cho NOT. Chúng ta gọi chúng NOT là cổng - chúng tôi gọi chúng là cổng vì chúng kiểm soát đường đi của dòng điện của chúng ta.




AND gates 

 AND Boolean nhận hai đầu vào, nhưng vẫn có một đầu ra duy nhất. Trong trường hợp này, đầu ra chỉ đúng nếu cả hai đầu vào đều đúng, Hãy nghĩ về nó như nói sự thật, Bạn chỉ hoàn toàn trung thực nếu bạn không nói dối dù chỉ một chút. Nếu tôi đảo ngược lời đó thì rõ ràng nó vẫn là sai, và nếu tôi nói với bạn hai lời nói dối hoàn toàn cũng sai, và một lần nữa chúng ta có thể viết tất cả những sự kết hợp này.
Để xây dựng một cổng AND, chúng ta cần hai bóng bán dẫn được kết nối với nhau để chúng ta có hai đầu vào và một đầu ra.
Nếu chúng ta chỉ bật bóng bán dẫn A, dòng điện sẽ không chạy vì dòng điện bị bóng bán dẫn B dừng lại .Nếu chúng ta chỉ bật bóng bán dẫn A, dòng điện sẽ không chạy vì dòng điện bị bóng bán dẫn B dừng lại.Ngoài ra, nếu bóng bán dẫn B đang bật, nhưng bóng bán dẫn A lại tắt. Chỉ khi bóng bán dẫn A VÀ bóng bán dẫn B đang bật thì dây đầu ra mới có dòng điện.
3.OR 
OR gate

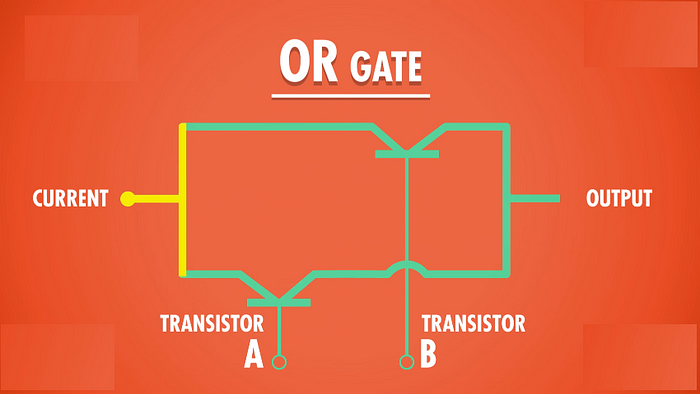
Boolean cuối cùng là OR- Trong đó chỉ có một đầu vào đúng thì đầu ra là đúng. Ví dụ: Nếu trời hôm nay có mây đen hoặc (OR) chuồn chuồn bay thấp, suy ra trời hôm hôm nay sẽ mưa. Vì vậy câu lệnh tổng thể là đúng một câu lệnh OR cũng đúng nếu cả hai sự kiện đều đúng. Lần duy nhất một câu lệnh OR là sai nếu cả hai đầu vào đều sai. Xây dựng một cổng OR từ các bóng bán dẫn cần thêm một vài dây. Thay vì có hai bóng bán dẫn mắc nối tiếp - nối tiếp nhau - chúng ta mắc chúng song song. Chúng ta chạy dây từ nguồn hiện tại đến cả hai bóng bán dẫn. Bây giờ nếu chúng ta chỉ bật bóng bán dẫn A, dòng điện có thể chạy đến đầu ra, điều tương tự nếu bóng bán dẫn A tắt, nhưng bóng bán dẫn B đang bật. Về cơ bản nếu A OR B đang bật, đầu ra cũng bật
Nếu chúng ta suy nghĩ về chúng theo cách này sẽ cho phép chúng ta xây dựng các thành phần lớn hơn nữa( bigger components). Trong khi giữ cho độ phức tạp tổng thể tương đối giống nhau - chỉ cần nhớ rằng các bóng bán dẫn và dây dẫn vẫn ở đó. Ví dụ. một phép toán Boolean hữu ích khác trong tính toán được gọi là phép Exclusive OR -hoặc XOR . XOR giống như OR thông thường, nhưng có một điểm khác biệt: nếu cả hai đầu vào đều đúng, thì XOR là sai. nếu cả hai đầu vào là đúng, thì XOR là sai. Lần duy nhất một XOR đúng là khi một đầu vào là đúng và đầu vào còn lại là sai. Nó giống như khi bạn đi ăn tối và bữa ăn của bạn có salad HOẶC súp - thật đáng buồn, bạn không thể có cả hai.



Việc xây dựng điều này từ các bóng bán dẫn khá khó hiểu, nhưng chúng tôi có thể cho thấy cách một XOR được tạo ra từ ba cổng Boolean cơ bản của chúng ta. Chúng ta biết rằng chúng ta lại có hai đầu vào -A và B và một đầu ra, Hãy bắt đầu với cổng OR, vì bảng logic trông gần giống với OR, Chỉ có một vấn đề - khi A và B là đúng, logic khác với OR và chúng ta cần xuất ra "false" Để làm được điều này, chúng ta cần thêm một số cổng bổ sung. nếu chúng ta thêm một cổng AND và đầu vào là true, thì đầu ra sẽ là true. Đây không phải là những gì chúng ta muốn, nhưng nếu chúng ta thêm NOT ngay sau đó sẽ chuyển nó thành false. Được rồi, bây giờ nếu chúng ta thêm một cổng AND cuối cùng và gửi cho nó giá trị nào cùng với đầu ra của cổng OR ban đầu của chúng tôi, AND sẽ nhận trong "false" và "true", và vì AND cần cả hai giá trị là true, đầu ra của nó là sai. Đó là hàng đầu tiên của bảng logic của chúng tôi. XOR hóa ra là thành phần rất hữu ích.

Hình hơi xấu , mọi người thông cảm @@

Quan trọng nhất, bây giờ chúng ta có thể đặt XOR vào hộp công cụcủa mình và không phải lo lắng về các cổng logic riêng lẻ tạo nên nó, hoặc các bóng bán dẫn tạo nên các cổng đó hoặc cách các electron chạy qua một chất bán dẫn. Chuyển lên một lớp trừu tượng khác khi các kỹ sư máy tính thiết kế bộ xử lý, họ hiếm khi làm việc ở cấp độ bóng bán dẫn, thay vào đó làm việc với các khối lớn hơn nhiều như cổng logic, và thậm chí các thành phần lớn hơn, được tạo thành từ cổng logic.

Ngay cả khi bạn là một lập trình viên máy tính chuyên nghiệp, không mấy khi bạn nghĩ về cách logic mà bạn đang lập trình thực sự được thực hiện trong thế giới vật lý bởi những thành phần nhỏ xíu này.
Chúng ta cũng đã chuyển từ suy nghĩ về các tín hiệu điện thô sang biểu diễn đầu tiên của chúng tôi về dữ liệu - đúng và sai - và chúng ta thậm chí đã có một chút hương vị về tính toán. Chỉ với các cổng logic trong tập này, chúng ta có thể xây dựng một máy đánh giá các câu lệnh logic phức tạp. như Nếu "Tên là Jayson VÀ sau 5 giờ chiều OR là Cuối tuần AND gần tiệm cơm tự chọn" thì " Jayson sẽ muốn ăn cơm tự chọn " bằng true.