Nhập môn toán xác suất

Nếu bạn mong muốn xây dựng một hệ thống Game hóa mang yếu tố may mắn (Core Drive 7), ví dụ như các minigame dạng slot-machine hay các hệ thống gashapon khác, thì những kiến thức cơ bản về toán xác suất là vô cùng cần thiết.

Chúng ta hầu như ai cũng nắm được sơ sơ về xác suất, nhưng rất nhiều những người mới chân ướt chân ráo bước vào thiết kế Game hóa lại thiếu những công cụ để phân tích những hệ thống dù là đơn giản nhất trong sản phẩm của mình một cách khoa học. Và bài viết này sẽ giới thiệu sơ qua về lý thuyết này.

Lý thuyết xác suất trên thực tế được hình thành bởi những người chơi game. Họ muốn hiểu thật rõ các tỷ lệ trong các game có khả năng may rủi. Và nhờ có game, mà mảng toán xác suất mới phát triển đến được như ngày nay.

Trong lý thuyết xác suất, chúng ta nói đến “tỷ lệ” xảy ra của một điều gì đó, được thể hiện bằng một con số giữa 0% và 100% (hoặc 0 và 1). Nếu tỷ lệ để A xảy ra là 100%, thì A chắc chắn sẽ xảy ra. Nếu tỷ lệ là 50%, thì khả năng A xảy ra và không xảy ra là như nhau.

Để hiểu được đúng bản chất của việc này, chúng ta cần phải biết đưa ra những câu hỏi hết sức cụ thể. Nếu tôi chơi tung xúc xắc, thì tỷ lệ ra ngửa là bao nhiêu? Điều này sẽ phụ thuộc vào việc bạn muốn trả lời câu hỏi gì. Bởi nếu như bạn chỉ tung đồng xu một lần, thì chúng ta có thể cho rằng tỷ lệ ra mặt ngửa là 50%. Nhưng nếu bạn ngồi cả ngày để tung đồng xu, thì tỷ lệ bạn tung ra mặt ngửa sẽ gần như là 100%.

Nếu bạn lấy tất cả các kết quả có thể xảy ra của một sự kiện ngẫu nhiên nào đó và cộng dồn chúng lại, thì tổng của chúng luôn là 100%. Ví dụ, khi bạn tung một đồng xu, thì tỷ lệ đồng xu nằm ở mặt ngửa (50%) cộng với tỷ lệ đồng xu nằm ở mặt sấp (50%) luôn ra kết quả là 100%.

Với hai lần tung đồng xu, thì có tổng cộng 4 khả năng có thể xảy ra: SS, NN, SN, NS. Mỗi khả năng có cùng tỷ lệ là 25%.

Xúc xắc hay còn gọi là xí ngầu. Trong khuôn khổ bài viết xin phép được sử dụng từ xúc xắc.

Tỷ lệ ra số 6 khi thảy một xúc xắc 6 mặt (hay còn gọi là d6) là bao nhiêu? Chắc chắn là ⅙ rồi. Và điều này có thể được gọi là “một phần sáu” hay “một trong sáu”, và rơi vào khoảng 16.7%.

Thế còn tỷ lệ thảy ra một số hay một tập số bất kỳ nào đó trên xúc xắc d6 là bao nhiêu? Mỗi số đều có tỷ lệ giống nhau là 1/6. Bởi vì tất cả tỷ lệ đều riêng biệt và không phụ thuộc vào nhau, nên bạn có thể cộng chúng vào với nhau, ví dụ như tỷ lệ rơi ra một trong số hai mặt số 4 và 5 sẽ là 1/6 + 1/6 = 1/3.

Bạn cũng có thể tìm được tỷ lệ của một số hay một tập số bằng cách lấy 1 và trừ đi tỷ lệ ngược lại. Do đó, tỷ lệ thảy ra được một số bất kỳ trừ số 6 trên xúc xắc d6 sẽ là 1 - 1/6 = 5/6.

Trong game Pairs, mục tiêu của trò chơi là tránh việc bốc phải một đôi (hai lá bài cùng cấp). Các lá bài trong bộ bài Pairs đều được phân bổ theo cấp số nhân: 1x1, 2x2, 3x3 cho tới 10x10. Ngoài ra không còn lá nào khác. Tổng số các lá bài là 55. Và câu hỏi ở đây là: nếu trên tay bạn đang cầm hai lá bài là 9 và 10 và bạn bốc tiếp một lá lên, thì tỷ lệ có được một đôi cùng cấp trên tay là bao nhiêu?

Trừ hai lá bài bạn đang cầm, thì trong bộ bài còn 53 lá. Trong số 53 lá này, còn có 8 lá bài số 9 và 9 lá bài số 10. Như thế có nghĩa là có 17 lá bài trong số 53 lá bài còn lại mà có thể tạo ra cho bạn một đôi. Và tỷ lệ sẽ là 17/53 tức tương đương khoảng 32%.

Tỷ lệ xuất hiện cùng một lúc (hoặc lần lượt) của nhiều đối tượng có thể được xác định bằng cách nhân các tỷ lệ riêng lẻ của chúng với nhau. Ví dụ, tỷ lệ tung đồng xu hai lần liên tiếp ra mặt ngửa là 25%. Con số này có nghĩa là 50% của lần tung đầu tiên nhân với 50% của lần tung tiếp theo. Tỷ lệ của ba lần tung đồng xu liên tiếp ra mặt ngửa sẽ là 50% x 50% x 50% = 12.5%. Các tỷ lệ này cũng có thể được biểu diễn dưới dạng phân số là 1/2, 1/4, 1/8 và tương tự.

Cần lưu ý là phương pháp phân tích này chỉ đúng đối với các tình huống trong tương lai và chưa xảy ra. Nếu như bạn đã tung đồng xu hai lần liên tiếp được mặt ngửa, thì tỷ lệ của xảy ra của tình huống đó đã trở thành 100%, và tỷ lệ của lần tung tiếp theo ra mặt ngửa sẽ là 50%.

Kể cả nếu bạn phải thảy cả 3 xúc xắc cùng một lúc, thì khi tính toán bạn vẫn có thể hình dung như thể bạn thảy lần lượt từng xúc xắc một. Tỷ lệ rơi trúng mặt số 5 hoặc số 6 với xúc xắc đầu tiên là 2/6 (tức ⅓). Tỷ lệ là ⅓ với mỗi lần thảy xúc xắc, do đó kết quả sẽ là ⅓ x ⅓ x ⅓ = 1/27.

Để thắng một game trong trò chơi “Roll Six Times” (Thảy sáu lần), bạn phải thảy một xúc xắc d10 tổng cộng sáu lần. Mỗi lượt, bạn cần phải thảy ra được một số lớn hơn số lượt hiện tại. Ví dụ, ở lượt thứ 3, bạn phải thảy ra số 4 hoặc cao hơn. Nếu bạn thảy ra số thấp hơn số lượt hiện tại, bạn thua. Vậy đây có phải là game dễ?

Ở lượt thứ 1, bạn phải thảy ra số 2 hoặc hơn. Tỷ lệ thành công ở đây là 9/10, tức 90%. Ở lượt 2, tỷ lệ thành công giảm xuống 80%, và tương tự. Để thành công ở mỗi lượt, thì tỷ lệ sẽ là 90% x 80% x 70% x 60% x 50% x 40%, tức là khoảng 6%.

Bài tập dành riêng cho bạn: Nếu bạn có thể chọn được số mặt của xúc xắc, thì bạn sẽ cần một xúc xắc có ít nhất bao nhiêu mặt để tỷ lệ thắng trò chơi “Thảy sáu lần” là 50% trở lên?

Kết quả loại trừ nhau có nghĩa là các kết quả này sẽ không bao giờ xảy ra cùng một lúc. Ví dụ, sẽ không bao giờ có trường hợp đồng xu bạn tung lên ra được cả hai mặt sấp và ngửa. Trong một lượt tung, đồng xu chỉ có thể ra sấp hoặc ra ngửa.

Vậy thì các kết quả loại trừ nhau sẽ trông thế nào? Hãy thử nghĩ về bài toán tỷ lệ bốc ra một quân bài là “Hoặc là Át, hoặc là Nhép.” Trong một bộ bài có tổng cộng 13 lá bài Nhép và 4 lá bài Át, thì nếu tất cả các kết quả này đều thuộc dạng loại trừ lẫn nhau, thì sẽ có tổng cộng 17 tình huống thành công. Nhưng trên thực tế, thì chúng ta cần nhớ là có một cây Át Nhép, tức là thỏa mãn đồng thời cả hai điều kiện trên, do đó chúng ta không được phép tính lá bài này hai lần. Như vậy có nghĩa là thực ra chỉ có 16 tình huống thành công mà thôi.

Trong một ví dụ nhỏ như vậy, thì việc đếm các lần trúng và các lần trượt còn dễ. Nhưng với các tập dữ liệu lớn hơn thì không phải lúc nào cũng dễ dàng tính được các kết quả khả thi đâu nhé!

Với hai lần tung xúc xắc 10 mặt (2d10), tỷ lệ thảy ra số 10 ít nhất một lần là bao nhiêu? Cái cụm “ít nhất 1 lần” vốn đã bao hàm ba tập kết quả khác nhau: “10 và X”, “X và 10”, “10 và 10.” Và vì thế, có tổng cộng 19 khả năng để thành công. Đó là 9 trường hợp của “10 và X”, 9 trường hợp của “X và 10”, cộng thêm trường hợp “10 và 10” đơn lẻ nữa. Tổng số các trường hợp có thể thảy ra được với hai xúc xắc 10 mặt là 100 (10 x 10), và vì thế tỷ lệ thành công là 19/100, tương đương 19%.

Một cách khác để giải bài toán này là tìm những trường hợp THẤT BẠI, sau đó lấy 1 trừ đi tỷ lệ của chúng. Nếu bạn thất bại trong trò chơi “thảy ra ít nhất một con 10,” thì có nghĩa là bạn không ra một con 10 nào trong lần thảy đầu tiên (90%) và trong lần thảy thứ hai (90%). Và vì thế, tỷ lệ không ra một con 10 nào trong cả hai lần thảy sẽ là 0.9 x 0.9 = 0.81, tương đương 81%. Lấy 100% trừ đi tỷ lệ thất bại 81% này, ta có 19% là tỷ lệ thành công.

Toán xác suất thì bao giờ cũng dễ dàng hơn khi tất cả các kết quả khả thi đều có cùng xác suất. Ví dụ, mặt sấp và mặt ngửa có cùng tỷ lệ 50%; mỗi mặt số trên xúc xắc 6 mặt (d6) cũng có cùng tỷ lệ ⅙. Nhưng một số trường hợp khác thì lại không đơn giản như vậy. Với hai lần thảy xúc xắc 6 mặt, tỷ lệ thảy ra tổng số 2 thì thấp hơn tỷ lệ thảy ra tổng số 7 rất nhiều. Đó là bởi có rất nhiều tình huống để dẫn đến tổng số 7 hơn là tổng số 2.

Để hình dung được rõ hơn về các tỷ lệ này, thì đôi khi sẽ dễ dàng hơn nếu chúng ta chia nhỏ nó ra thành một danh sách các trường hợp đồng xác suất.

Kẻ cướp được di chuyển trong Catan như thế nào? Ở đầu mỗi lượt trong Catan, người chơi hiện tại sẽ thảy 2 xúc xắc 6 mặt (2d6) để xác định những vùng nào sẽ sản xuất tài nguyên. Khi thảy ra tổng số là 7, thì không có tài nguyên nào được sản xuất, và kẻ cướp sẽ được di chuyển. Do đó, câu hỏi ở đây là tỷ lệ ra số 7 trên xúc xắc 2d6 là bao nhiêu?

Có tổng cộng 36 kết quả cho xúc xắc 2d6. Trong số đó, có tổng cộng 6 tình huống để ra được tổng số 7. Đó là (1,6), (2,5), (3,4), (4,3), (5,2), và (6,1). Do đó,  khả năng để thảy ra tổng số là 7 trên xúc xắc 2d6 là 6/36, tức ⅙. Điều này có nghĩa là trung bình, kẻ cướp trong Catan sẽ được di chuyển một lần trong mỗi sáu lượt.

Các trường hợp độc lập thống kê là các trường hợp mà ở đó kết quả của một tình huống A không gây ảnh hưởng lên kết quả của tình huống B. Nhìn chung, đây chính là cách hoạt động của các trường hợp ngẫu nhiên. Khả năng bạn tung đồng xu ra mặt ngửa thì không bị ảnh hưởng bởi những lần tung đồng xu trước đó (hoặc bởi thời tiết, bởi chiêm tinh, hay niềm mong ước và ý chí chiến thắng lớn lao của bạn.)

Tuy nhiên, trong một số trường hợp, khả năng xảy ra của một tình huống có thể bị ảnh hưởng bởi kết quả của những tình huống trước đó. Việc này xảy ra khi tính ngẫu hứng bị thay đổi bởi các tình huống. Ví dụ điển hình nhất của khái niệm này là việc bốc bài từ một bộ bài. Mỗi lần bốc bài là bạn đã làm thay đổi các tỷ lệ khả thi của những lần bốc bài tiếp theo. Các game như thế này có thể tạo ra các tình huống phục thuộc thống kê.

Ví dụ, nếu bạn bốc hai lá bài từ một bộ bài poker, thì tỷ lệ quân bài thứ hai của bạn là quân Át sẽ là bao nhiêu? (Hãy so sánh bài toán này với bài toán “Thảy ra ít nhất một con 10” ở trên). Nếu quân bài thứ nhất là quân Át, thì tỷ lệ quân bài thứ hai là Át sẽ là 3/51. Nếu quân bài đầu tiên không phải là quân Át, thì tỷ lệ quân bài thứ hai là Át sẽ là 4/51.

Để tìm tỷ lệ bốc ra ít nhất một quân bài Át trong hai lượt bốc bài, chúng ta có thể đếm ra tất cả các tình huống thành công, tính tỷ lệ của chúng, sau đó cộng chúng lại với nhau để ra kết quả. Trong tình huống 1, quân bài đầu tiên là Át, thì chúng ta không cần quan tâm đến quân bài thứ 2 là gì, vì điều kiện đã được thỏa mãn. Và tỷ lệ của kết quả này là 4/52, tức khoảng 7.7%.

Trong tình huống 2, quân bài đầu tiên không phải là Át, nên chúng ta chỉ có thể thắng nếu quân bài thứ hai là Át. Tỷ lệ quân bài đầu tiên KHÔNG phải là Át là 100% - 7.7% = 92.3%. Tại đây, tỷ lệ để bốc ra được quân bài Át là 4/51, tức khoảng 7.8%.

Để tìm ra tỷ lệ thành công ở tình huống 2 này, chúng ta sẽ nhân hai tỷ lệ trên với nhau. Từ đó ta có kết quả 92.3% x 7.8% = 7.2%.

Bởi vì tình huống 1 và tình huống 2 là hai kết quả loại trừ nhau, chúng ta có thể cộng hai tỷ lệ này lại và được kết quả 7.2% + 7.7% = 14.9%.

Cũng giống như chúng ta đã nói với xúc xắc d10, một kết quả đơn giản hơn rất nhiều sẽ là cách tìm tỷ lệ của tình huống “không có quân Át nào”, sau đó lấy 1 trừ kết quả đó. Tỷ lệ không bốc trúng quân Át nào là 48/52 với quân bài đầu tiên, và 47/51 với quân thứ hai. Hai tỷ lệ này nhân với nhau ra 85.1%. Và ta có 100% - 85.1% = 14.9%.

Tuy nhiên, phần phân tích dài dòng ở trên lại có thể áp dụng được trong rất nhiều tình huống trong game, mà ở đó các bạn chỉ được phép tìm ra kết quả với dữ liệu không đầy đủ. Ví dụ, trong một game stud poker (biến thể của poker khi người chơi nhận được một nửa số bài của mình là lật ngửa, còn một nửa còn lại úp xuống) thì tỷ lệ xuất hiện của một số lá bài cụ thể sẽ phải dựa trên những lá mà người chơi đã biết.

Một khái niệm khá hữu ích nữa trong lý thuyết xác suất là “giá trị kỳ vọng.” Khái niệm này nghe qua thì có vẻ không trực quan lắm, bởi nó dựa trên các kết quả trung bình và có thể sẽ không đại diện cho một kết quả khả thi. Khái niệm này phản ánh hiệu năng trung bình của một chuỗi những lần thử dài.

Ví dụ, giá trị kỳ vọng của một xúc xắc d6 là trung bình của tất cả các kết quả đồng xác suất (1, 2, 3, 4, 5, 6), tức là  (1 + 2 +3 + 4 + 5 + 6) / 6 = 3.5. Tất nhiên, trên xúc xắc không có mặt nào là 3.5 cả, nhưng nếu bạn thảy một xúc xắc d6 cả triệu lần thì kết quả trung bình nhận được sẽ rất gần với con số 3.5.

Hãy hình dung một game đối đầu tính điểm mà ở đó một người chơi nhận miễn phí 7 điểm mỗi lượt, và người chơi còn lại được tính điểm bằng cách thảy xúc xắc d6 hai lần. Nếu là bạn thì bạn sẽ chọn phe nào? Cả hai phe đều có cùng giá trị kỳ vọng là 7, nhưng phe nào có lợi hơn? Điều này thường phụ thuộc vào ý thích cá nhân (hoặc phụ thuộc vào các cơ chế game khác),  và rất nhiều các ví dụ tương tự của những lựa chọn như thế này đều có trong các game khác.

Giá trị kỳ vọng trở nên hữu dụng trong những tình huống mà ở đó các giá trị số được tổng hợp lại, ví dụ như việc thảy xúc xắc tính điểm như ví dụ ở trên, hoặc khi theo dõi tổng số trận thắng và thua trong cờ bạc. Nếu bạn không sử dụng các giá trị số của xúc xắc, hoặc các mặt của xúc xắc không phải là số mà là cái gì đó khác mang tính biểu tượng, thì giá trị kỳ vọng là vô nghĩa.

Trong các game casino, giá trị kỳ vọng là một khái niệm vô cùng hữu ích.

Nếu chúng ta chơi một game mà ở đó bạn thảy một xúc xắc d6 và nhận $1 cho mỗi điểm bạn có, thì trung bình mỗi game bạn sẽ nhận được $3.50. Nếu là tôi thì tôi sẽ không ngu gì chơi game đó với bạn, trừ phi bạn sẵn sàng đánh cược $4 cho mỗi ván. Bởi nếu như vậy thì với bạn, giá trị kỳ vọng của game lúc này là -$0.50.

Với một game công bằng hơn, thì tôi có thể cho bạn thảy xúc xắc 2 lần nhưng phải cược $7. Giá trị kỳ vọng của xúc xắc 2d6 là 2 x 3.5 = 7, do đó với mức cược là $7 và giá trị kỳ vọng là 7, thì tổng số giá trị kỳ vọng của cả hai phe là 0, và đó là một game công bằng với cả hai người.

Các game casino ngoài đời thường ra luật sao cho nhà cái có một chút lợi thế, thường rơi vào khoảng $.050 lợi nhận trên mỗi ván cược $4. Ví dụ dưới đây cho thấy một lợi thế như vậy được đặt ra như thế nào.

Cược một chọi (field bet) là một dạng cược để thảy xúc xắc đúng 1 lần, được ăn cả và ngã về không. Nếu lần thảy tiếp theo của bạn ra 3, 4, 9, 10 hoặc 11, bạn sẽ thắng được số tiền bằng 1x số tiền bạn cược. Nếu bạn thảy ra 2 hoặc 12, bạn thắng x2. Mọi kết quả còn lại (5, 6, 7, 8) bạn sẽ thua. Vậy kèo này có thơm không? Và chúng ta biểu diễn độ thơm của kèo này như thế nào?

Trước hết, hãy nhìn vào giá trị kỳ vọng của kèo. Có tổng cộng 36 kết quả khác nhau cho xúc xắc 2d6, với tổng giá trị và tỷ lệ được liệt kê trong bảng ở dưới. Cột “Ways” biểu thị những khả năng khác nhau để tạo ra được một tổng. Ví dụ, có tổng cộng 6 khả năng để tạo ra được tổng 7 (như chúng ta đã nhắc đến trong ví dụ về Catan).

Cột tiếp theo là “Pays” biểu thị giá trị số nhân của số tiền bạn nhận được. Lưu ý là nếu bạn thua, giá trị này sẽ là 0, tức là bạn không nhận được tiền. Nếu bạn thắng 1 ăn 1, thì giá trị tiền bạn cầm về sẽ là 2, bởi vì bạn cầm về cả tiền cược của bạn và tiền thắng cược của nhà cái. Tương tự, khi bạn thắng 2 ăn 1, giá trị tiền sẽ là 3.

Cột cuối cùng, “Value,” là kết quả của Ways và Pays. Đây là giá trị tổng của tất cả các khả năng của mỗi kết quả. Ví dụ, có tổng cộng 2 cách để ra kết quả là 3, và giá trị thưởng của kết quả này là 2, vậy thì giá trị của kết quả này là 2 x 2 = 4. Tính tổng giá trị của tất cả các kết quả, ta có tổng là 34.

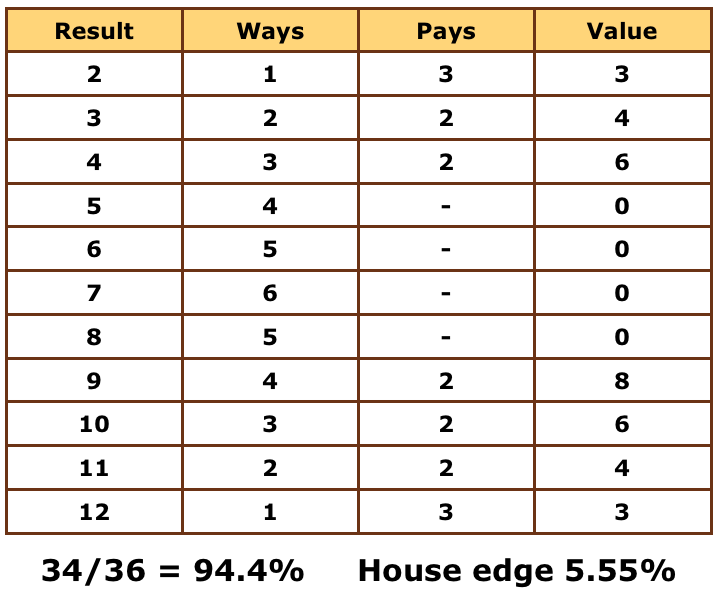
Lưu ý rằng ở đây, chúng ta sẽ giả sử chúng ta chơi 36 lần và mỗi lần lại ra một kết quả trong số 36 kết quả khả thi khác nhau, sau đó cộng tổng các kết quả lại. Việc này cũng giống như việc chúng ta tính giá trị trung bình của tất cả các kết quả khả thi của việc thảy xúc xắc d6 để ra giá trị kỳ vọng của xúc xắc vậy. Trong trường hợp này, chúng ta có thể thấy rằng sau khi chơi 36 lượt Cược một chọi, tổng giá trị chúng ta thu về là 34.

Tuy nhiên, mỗi ván cược chúng ta phải bỏ tiền cược một lần, do đó tổng chi phí chúng ta phải bỏ ra là 36, như vậy có nghĩa là trung bình mà nói, chúng ta thiệt mất 2 giá trị. 2 giá trị này quy đổi ra tỷ lệ là 2/36, tức là khoảng 5.55%. Tỷ lệ này chính là “house edge” (lợi thế của nhà cái.)

Rất may là hầu hết các ván Cược một chọi ngoài đời thì thơm hơn chút, và sẽ trả cho bạn gấp ba (chứ không phải gấp hai) số tiền cược khi bạn thảy ra 12. Việc này sẽ thay đổi tỷ lệ như thế nào? Tại đây, Cột Pays và Value của 12 sẽ trở thành 4 (3 tiền thưởng và 1 tiền cược). Tổng giá trị trung bình của game sẽ trở thành 35/36, và lợi thế của nhà cái sẽ tụt xuống một nửa, từ 2/36 thành 1/36, tức là xuống còn 2.78%.

Một quan niệm sai lầm về các sự kiện ngẫu nhiên đó là kết quả của chúng sẽ có xu hướng “tự cân bằng” sau một khoảng thời gian. Đây được gọi là ngụy luận của con bạc (Gambler’s Fallacy). Ví dụ, sau khi tung đồng xu mấy lần đều ra mặt ngửa, thì tỷ lệ ra mặt sấp sẽ bằng cách nào đó tăng lên. Nếu các kết quả là hoàn toàn độc lập về thống kê, ví dụ như khi tung đồng xu, thì điều này là không đúng.

Và kể cả khi bạn không hiểu lầm chuyện này, thì bạn vẫn có thể sẽ nghĩ rằng việc bổ sung thêm các sự kiện ngẫu nhiên sẽ giúp tiêu giảm hiệu ứng bất công của những sự kiện ngẫu nhiên trước đó. Đây là một dạng “tính năng lật ngược” được thiết kế để cho những người chơi xấu số có thêm hy vọng. Tuy nhiên, cách này thường không hiệu quả. Có thêm các lựa chọn thì tốt, có thêm sự kiện ngẫu nhiên thì không. Đây là lý do vì sao các game thuần may rủi thường kết thúc rất sớm.

Tôi vừa thảy xúc xắc d6 sáu lần, và lần nào cũng ra con 6. Vậy ở lần thảy tiếp theo, tỷ lệ ra con 6 sẽ tăng lên hay giảm đi? Có phải con 6 đang “vào cầu” và tôi sẽ có nhiều cơ hội thảy được con 6 hơn không, hay là tôi đã “dùng hết nhân phẩm” rồi?

Câu trả lời: Sai hết. Xúc xắc không có hoạt động như vậy. Tỷ lệ thảy ra con 6 không bao giờ có thể bị thay đổi bởi kết quả trước đó. Không giống như với một bộ bài, mà ở đó những lá bài bốc lên trước đó sẽ thay đổi tỷ lệ của những lá bài còn lại. Và cái ngụy luận của một con bạc chính là niềm tin rằng xúc xắc thì hoạt động như bộ bài vậy.

Tùy thuộc vào mức độ phức tạp trong hệ thống Game hóa của bạn mà bạn có thể phân tích hoàn toàn tất cả các yếu tố ngẫu nhiên trong đó được hay không. Dù vậy thì lý thuyết xác suất vẫn vô cùng hữu ích khi bạn cần phân tích một số phần nhỏ trong hệ thống của mình. Bằng cách đó, bạn sẽ phần nào hiểu được rõ hơn những tình huống nào có thể, hoặc hiếm khi, hoặc không bao giờ xảy ra.

Bạn có thể xây dựng một bộ công cụ tự động để test hệ thống trên scale lớn. Nhưng đến cuối cùng thì bạn vẫn cần phải có khả năng phân tích các số liệu nhận được để xác định xem kết quả có khớp với những gì bạn hình dung khi thiết kế ban đầu hay không.

Hiểu biết của đối tượng người chơi (VD: nhân viên, khách hàng, người học) về toán xác suất thì thường là không quá tệ, nhưng họ lại không có những công cụ để phân tích tại chỗ. Vì thế, việc quan trọng bạn cần làm là giải thích tính ngẫu nhiên cho họ càng rõ ràng càng tốt để giúp cho họ thấy rằng trải nghiệm của họ ăn khớp với kỳ vọng. Nếu một thử thách ngẫu nhiên trông rất dễ, nhưng trên thực tế lại rất khó hoặc bất khả thi, thì trải nghiệm với hệ thống Game hóa của bạn sẽ trở nên vô cùng ức chế.

Một lời khuyên là tốt hơn hết bạn hãy để cho người chơi có cơ hội suy nghĩ và cân bằng những rủi ro, thay vì bị phụ thuộc hoàn toàn vào may rủi. Đó là lý do vì sao các quyết định của họ phải là những quyết định thật, có trọng lượng và có tính toán.