Bạn mình làm Data Analyst, bữa nó nhắc đến đạo hàm tích phân trong lúc xây dựng model tính toán cho project của nó. Hai cái chữ đạo hàm tích phân này hồi đi học nghe hoài, làm bao nhiêu bài tập. Thi đại học có cái câu khảo sát hàm số, hầu như ai cũng làm được hết. Nhưng giờ nếu ai đó hỏi mình ủa rồi bản chất Đạo hàm là gì, tại sao phải sinh ra nó, nó có ứng dụng gì cho đời, hay có ứng dụng gì trong việc phân tích lúc đi làm thì mình lại không trả lời được. Mình Google đạo hàm là gì, kết quả trả về như sau:
“Đạo hàm của một hàm số là một đại lượng mô tả sự biến thiên của hàm tại một điểm nào đó”, đi kèm là các công thức tính toán Đạo hàm. Với mình cái này vẫn chưa đủ dễ hiểu và dễ nhớ, từ nhỏ đến lớn mình chưa bao giờ học giỏi Toán. Nên mình cố gắng tìm các cách giải thích dễ hiểu dễ nhớ hơn. Mình note lại ở đây những cái mình hiểu bao gồm: (1) Đạo hàm là gì; (2) Nó có ứng dụng gì mà phải sinh ra một khái niệm trừu tượng như vậy; (3) Trong data analysis/data science thường dùng đạo hàm để làm gì? Bài này nói về chủ đề Toán nhưng sẽ dùng chữ nhiều hơn là số hay công thức tính đạo hàm, công thức học cả mấy năm cấp ba rồi, giờ cũng có hiểu bản chất đạo hàm là gì đâu mà chú trọng công thức tính toán làm gì nữa.

Đạo hàm là gì?

Hiểu đơn giản Đạo là con đường hay đường đi. Hàm là hàm số. Đạo hàm có nghĩa là đường đi của hàm số. Thế để hiểu đạo hàm là gì thì phải hiểu hàm số nghĩa là gì trước đã.

Thế hàm số là gì?

Công ty trả lương cho nhân viên bán hàng với cơ chế như sau: Mỗi nhân viên sẽ nhận được lương fix 5 triệu 1 tháng, nếu bán thêm mỗi cái áo thì sẽ được 10k.
Nhân viên A bán được 10 cái áo, lương sẽ là 10k*10 cái áo + 5tr = 5.100.000đ
Nhân viên B bán được 20 cái áo, lương sẽ là 10k*20 cái áo + 5tr = 5.200.000đ
Vậy hàm số để mô tả cho cơ chế tính lương như trên sẽ là f = 10k*x + 5tr (vnđ). Trong đó f sẽ là tiền lương nhân viên một tháng và x là số áo nhân viên đó bán được trong một tháng. Hàm có nghĩa là bao hàm. Một hàm số được biểu diễn để bao hàm được hết các trường hợp xảy ra.
Đây là ví dụ về một hàm số tuyến tính đơn giản, thuộc nhóm những Hàm số cơ bản mình được học ở cấp ba. Trong thực tế sẽ có những hàm số phức tạp hơn như vậy rất nhiều. Ví dụ hàm số f nào thể hiện giá trị của một căn nhà khi có các yếu tố đầu vào (diện tích, số phòng ngủ, hướng, khu đất, năm xây dựng, thị trường, tỉ lệ lạm phát…). Hay hàm số f để xác định giá chứng khoán ngày mai.
Rồi bây giờ quay lại câu hỏi
Đạo hàm là gì?
Đạo hàm dùng để mô tả sự biến thiên của hàm số. Quay lại ví dụ tính lương bên trên: Nếu bán được thêm 1 đơn vị (cái áo), thì tiền lương sẽ tăng/giảm bao nhiêu? Hay nếu tỉ lệ lạm phát tăng thêm 1 đơn vị thì giá nhà sẽ thay đổi như thế nào? Hay hiểu đơn giản, ý nghĩa của đạo hàm ở đây là: Khi nào có sự thay đổi, ta có thể xem được hàm số đó sẽ thay đổi như thế nào bằng đạo hàm (thay đổi bao nhiêu, tốc độ thay đổi). Khi đọc phần ứng dụng thực tiễn của đạo hàm bên dưới, sẽ dễ hình dung và hiểu rõ hơn đạo hàm là gì.

Đạo hàm dùng để làm gì?

Đạo hàm có 2 ứng dụng quan trọng như sau
Ứng dụng 1: Đạo hàm dùng để tìm giá trị lớn nhất và nhỏ nhất của một hàm số.
Sau khi có hàm số (f). Bằng cách tìm đạo hàm của hàm số. Bạn sẽ tìm được giá trị cực đại (giá trị lớn nhất), hay cực tiểu(giá trị nhỏ nhất) của hàm số đó bằng cách tìm điểm mà tại đó đạo hàm bằng 0.
Ví dụ: Hình bên dưới mô tả hàm bậc hai (y=-x^2+4x-4). Để tìm được điểm cực đại của hàm này chỉ cần tìm đạo hàm của hàm này. Sau đó xem tại đạo hàm y'(x) = 0 thì điểm x bằng bao nhiêu, điểm đó sẽ là cực đại.
Với ví dụ này, áp dụng công thức đạo hàm của hàm bậc hai, ta tìm được y’ = -2x + 4. Để tìm cực trị, ta cho y’= 0 hay -2x + 4 = 0, suy ra tại điểm x = 2, y đạt giá trị cực trị.
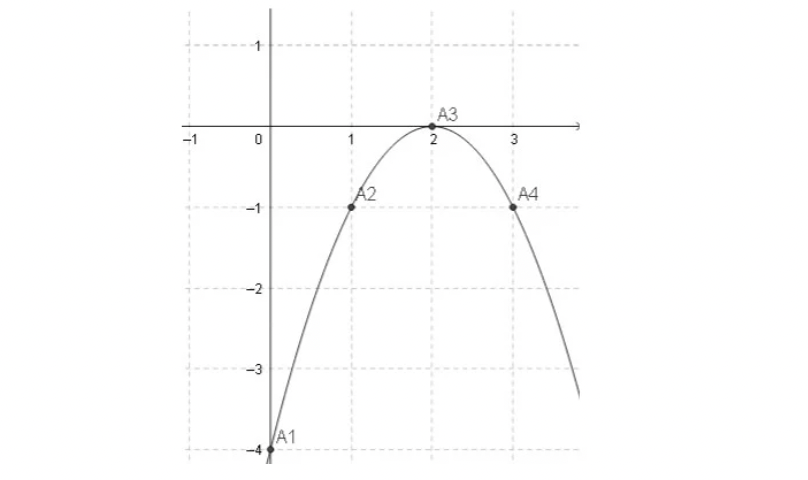
Tuy nhiên có bạn sẽ hỏi cần gì biết đạo hàm làm gì, chỉ cần nhìn hình vẽ bên trên cũng thấy được tại điểm x = 2 thì giá trị hàm số là lớn nhất. Hoặc ngồi thay số lần lượt vào, thay đến lúc thấy giá trị y là lớn nhất thì lúc đó biết được tại x bằng mấy thì y là cực đại thôi.
Nhưng trên thực tế, không phải bài toán nào cũng đơn giản như cái hàm bậc hai trên. Ví dụ:
Giả sử bạn làm việc cho Shopee, bạn cần phân tích nên tặng cho một khách hàng bao nhiêu voucher để maximize lợi nhuận của tháng 12 cuối năm của công ty. Giả sử ta có hàm f nào đó mô tả lợi nhuận thu được từ khách hàng của tháng 12 qua: số tiền khách hàng chi tiêu mỗi tháng, tuổi của khách hàng, số voucher khuyến mãi Shopee tặng khách hàng vào tháng 12, thu nhập của khách hàng đó, khu vực sinh sống của khách hàng… Bạn muốn tính số voucher khuyến mãi Shopee tặng cho mỗi khách hàng cụ thể là bao nhiêu để lợi nhuận công ty là tối đa. Mỗi khách hàng mỗi đặc điểm khác nhau, khuyến mãi nhiều quá thì chắc chắn là lỗ, còn khuyến mãi ít quá thì khách hàng không chịu mua, khách hàng không mua thì cũng ảnh hưởng đến lợi nhuận.
Giả sử ta xây dựng được một hàm f mô tả như trên. Để tìm điểm cực đại của hàm f (điểm mà lợi nhuận vào tháng 12 của Shopee là cao nhất), ta có thể tìm được đạo hàm của hàm f. Sau đó cho đạo hàm f’ đó bằng 0 thì sẽ tìm ra giá trị cần tìm.
Vậy câu hỏi tiếp theo là công thức tính đạo hàm ở trường hợp của Shopee là gì? Thực ra việc tính đạo hàm ở đây không phức tạp bằng câu chuyện làm sao để xây dựng được một hàm số f “bao hàm” được các tính chất trên (Phần ứng dụng đạo hàm vào analysis bên dưới mình sẽ nói rõ hơn về cái này). Quay lại câu chuyện tính đạo hàm. Đạo hàm có công thức cơ bản là: Đạo hàm một tổng bằng tổng các đạo hàm. Gặp một hàm phức tạp hơn, người ta sẽ tách ta tính đạo hàm các hàm đơn giản hơn rồi sau đó tính tổng.
Thế công thức tính đạo hàm hàm cơ bản là gì. Cái này chỉ cần Google công thức để xem, hoặc đơn giản có máy tính tính rồi. Tới đây bắt đầu nhớ ra cái bảng công thức tính đạo hàm của mười mấy cái hàm số cơ bản. Ví dụ công thức đạo hàm hàm bậc hai, hàm bậc ba, hàm lượng giác… mà mọi người dành cả thanh xuân học thuộc lòng vẫn không hiểu học cái này lớn lên để làm gì hết.
Ứng dụng 2: Đạo hàm dùng để tính tốc độ thay đổi (rate of change) của một hàm số.
Đạo hàm có tính chất: Nếu hàm số đang tăng đạo hàm sẽ dương, tăng càng nhanh thì đạo hàm càng lớn. Ngược lại, hàm số đang giảm, đạo hàm sẽ âm và âm càng nhiều khi hàm số giảm càng nhanh.
Ví dụ nhìn lại cái hàm bậc 2 ban nãy, với điểm cực đại là A3, khi x di chuyển từ 1 đến 2 thì y sẽ di chuyển từ -1 đến 0. Từ điểm A2 đến A3, hàm số đang tăng, đạo hàm sẽ dương, hàm số tăng càng nhanh (hay độ dốc càng lớn) thì đạo hàm càng lớn. Khi hàm số đang tăng (đạo hàm dương) khi x di chuyển từ A2 đến A3 rồi bất chợt chuyển sang giảm (đạo hàm âm), nó đã đi qua vị trí mà tại đó hàm số đạt giá trị cực đại (là điểm A3)
Giả sử bạn xây dựng được một hàm dự đoán giá cổ phiếu được mô tả dưới dạng y = f (x). Trong đó x là đơn vị thời gian nắm giữ cổ phiếu đó, ví dụ ở đây mình tính theo giờ. Nếu bạn tính được đạo hàm y’ trên và thấy đạo hàm dương, bạn sẽ biết được y đang tăng, có thể bạn chưa nên bán vội, đạo hàm càng lớn thì giá trị của y càng cao hay giá cổ phiếu của bạn đang trong pha tăng với biên độ cao.

Thế trong data analytics/data science, thường dùng đạo hàm để làm gì?

Quay lại với ví dụ về Shopee ban nãy. Ta có Y = f (X) Trong đó: Y là lợi nhuận Shopee thu được từ khách hàng và X = (X1, X2, X3…Xn) X là các đặc điểm của khách hàng như: Số tiền khách hàng chi tiêu mỗi tháng, tuổi của khách hàng, số voucher khuyến mãi Shopee tặng khách hàng vào tháng 12, thu nhập của khách hàng đó …f là một unknow function (hàm mà ta chưa xác định được).
Trong thực tế, các giá trị của x thường sẽ có sẵn, nhưng rất khó để từ x ta tìm ra được giá trị y. Người ta sẽ cố gắng đi tìm hàm y* = f*(x), trong đó y* là giá trị dự đoán của y, còn f* là hàm dự đoán của f. Lúc này lại có thêm một khái niệm là Loss function hay còn gọi là hàm mất mát. Loss function thể hiện mối quan hệ giữa y* và y, hay giữa giá trị dự đoán và giá trị thực tế. Mục tiêu sẽ là làm sao đưa Loss function càng về 0 càng tốt hay tìm giá trị cực tiểu của hàm loss function, và ở đây ta sẽ áp dụng các ứng dụng của đạo hàm.
Giá trị cực tiểu của hàm loss function tạm gọi là global min, giá trị cực đại thì gọi là global max. Tại các điểm có đạo hàm = 0 sẽ là local min hoặc local max. Trong các local min, điểm nào thấp nhất sẽ là global min, điểm nào cao nhất của các local max sẽ là global max. Tuy nhiên vì sự phức tạp của dạng đạo hàm và các điểm dữ liệu, việc tính đạo hàm theo các này cũng cực kì khó khăn. Nên người ta lại có một hướng tiếp cận khác: Chọn một điểm đầu tiên, sau đó dùng một phép toán lặp để tiến dần đến điểm cần tìm, tức đến khi đạo hàm gần với 0.
+ Nếu tại x1 đạo hàm >0, có nghĩa là giá trị hàm số đang tăng, vì ta đang cần tìm giá trị cực tiểu, nên ta sẽ nhích x1 về bên trái hàm số.
+ Nếu tại x1 đạo hàm <0, có nghĩa là giá trị hàm số đang giảm, vì ta đang cần tìm giá trị cực tiểu nên ta sẽ nhích về bên phải x1 hàm số.
Điểm global min phụ thuộc vào hai yếu tố chính: Điểm đầu tiên chọn như thế nào (gọi là điểm khởi tạo) và tốc độ nhích tiếp theo (gọi là learning rate) là bao nhiêu.
Khi xác định được giá trị global min hay cực tiểu của hàm loss function, ta sẽ tìm được hàm f*, là hàm số gần đúng nhất tìm được của hàm f, hay hàm số ta đang tìm để mô tả lợi nhuận Shopee thu được từ một khách hàng với các yếu tố đầu vào cho trước như ví dụ ở bên trên.