Đừng lo lắng nếu bạn thấy toán học khó
Đó là kỷ niệm năm tôi học lớp mười một. Tôi vẫn nhớ, khi ấy thằng bạn Văn Phúc giấu tên học chung lớp với tôi rơi vào lo âu, căng thẳng,...
Đó là kỷ niệm năm tôi học lớp mười một. Tôi vẫn nhớ, khi ấy thằng bạn Văn Phúc giấu tên học chung lớp với tôi rơi vào lo âu, căng thẳng, ngụp lặn giữa biển chữ số và công thức. Đầu tóc cậu rối bời, chán nản, buông xuôi trước những bài toán được giao về nhà, có khi còn cấp bách hơn là khi anh ấy mất phương hướng, lạc lối, khó khăn trong việc tìm lại niềm cảm hứng say mê, cháy bỏng với môn toán ngày nào. Như một vị thần không mời mà đến, một ngọn hải đăng tự mọc lên chẳng ai hay, tôi tiến lại gần, rao giảng, chỉ dẫn, soi rọi, chữa lành tâm hồn con chiên của mình với những lời thiện ý rằng:
"Mày chớ sầu muộn, đừng run sợ khi thấy toán học khó vì đến cả nhà khoa học lừng danh như Albert Einstein đã từng phán: ‘Đừng lo lắng nếu bạn thấy toán học khó"

Tôi không biết lúc ấy thằng bạn tôi có thẩm thấu được câu nào không, nhưng tôi biết ba điều:
Một là, đôi mắt chú bé khi ấy đã bớt u ám, trong lòng hứng khởi trở lại và về sau, cậu còn lội ngược dòng, đá tôi ra khỏi top toán của lớp và của trường (vì suốt năm lớp mười hai tôi chỉ mãi đi ăn, đọc sách, và lảm nhảm mấy thuyết khoa học).
Hai là, tôi khi ấy cố tình cắt bớt khẩu phần trong câu nói của Einstein. Bởi nếu tôi thêm đoạn “. . . tôi còn thấy nó khó hơn bạn nhiều” thì quả là khập khiễng giữa một ông là vĩ nhân của nhân loại, còn một ông thì còn bị tôi đây cho leo cây dễ dàng. Nói ra e sẽ dẫn đến những hệ lụy, làm tổn thương chú bé, gây ra ý nghĩ tiêu cực, giảm tự tin vào bản thân, và biết đâu lại khiến thế giới mất đi một người làm Toán.
Điều cuối cùng tôi biết, là ý nghĩa thật sự về câu nói (đầy đủ nhé) của Einstein. Thật cảm kích và biết ơn nếu độc giả đã dành sự quan tâm đến bài viết này, khi bỏ ra hẳn một phút rưỡi cuộc đời chỉ để đi qua những thứ nhảm nhí, vô tội vạ như thế này. Nhưng với tôi, điều đó vẫn luôn là sự thật, vì rõ ràng ai mà chẳng có một ấn tượng huy hoàng lần đầu (như chú bé tôi vừa nhắc ở trên) với câu nói nghe qua tưởng chừng chỉ xoay quanh góc nhìn của việc học toán đơn thuần ở trường lớp chứ. Nếu chịu khó phân tích và xem xét lại bối cảnh của câu nói ấy, ta sẽ thấy câu nói đó còn ẩn chứa một vấn đề phát sinh lớn hơn về vật lý hiện đại đã tạo nên một hiện thực mới, ngày càng xa rời hiện thực của những ngày xa xưa.

Có hai bên ý kiến bàn luận về câu nói này của Albert Einstein.
Ý kiến đầu tiên cho câu nói này được bình luận bởi nhà toán học. Người ta thường cho rằng Einstein không hiểu sâu sắc toán học hoặc khi còn trẻ ông ấy học toán rất kém. Tuy nhiên thật là lầm lẫn khi nói rằng Einstein kém về môn toán. Một số bài báo của ông khá phức tạp về mặt toán học, liên quan đến các môn toán cao cấp như phương trình vi phân ngẫu nhiên và giải tích tensor. Hơn nữa, Einstein học toán rất xuất sắc khi còn trẻ. (Điều này đã được trình bày ở cuốn "Einstein: His Life and Universe" (có bản tiếng việt) do nhà sử học và nhà báo người Mỹ Walter Isaacson sáng tác).
Việc chuyển từ học toán học sơ cấp sang toán học cao cấp mang lại nhiều cảm giác bỡ ngỡ, chán nản ban đầu là điều thường thấy ở những người lần đầu tiếp xúc với nó vì mức độ nâng cao, phúc tạp về kĩ thuật đòi hỏi ở người học phải có sự tập trung cao độ, khả năng chịu khó, kiên nhẫn và đặc biệt là ý nghĩ vượt rào. Đây là điểm chính yếu cần lưu ý vì nếu các nhà toán học không vượt rào, vượt qua những đối tượng trực tiếp liên quan tới thế giới tự nhiên ở toán học sơ cấp, chỉ dựa trên những khái niệm cũ của những tiên đề sẵn có, thì sẽ chẳng mấy chốc toán học sẽ không còn định lý nào mới mẻ thú vị. Xây dựng những khái niệm nằm ngoài các tiên đề, được định nghĩa với tầm nhìn hướng tới những thao tác logic thông minh phù hợp với cảm quan của nhà toán học, cho ra những kết quả có tính bao quát và minh giản một cách tuyệt vời. Một ví dụ rất điển hình là số phức. Chắc chắn rằng các nhà toán học đưa ra khái niệm này mà không hề dựa trên một kinh nghiệm đời thực nào.
Có thể hiểu ý của Einstein theo góc độ nhà toán học rằng đó là một tuyên bố về những khó khăn trong toán học mà ông cảm thấy phải vật lộn để học một số kiến thức rất cao cấp cần thiết cho việc phát biểu các lý thuyết của mình, hoặc rằng so với với các nhà toán học hoặc nhà vật lý toán học, kĩ năng toán học của ông không hoàn toàn được coi là mẫu mực. Tuy nhiên, chắc chắn Einstein có năng khiếu toán học bẩm sinh vượt trội hơn rất nhiều so với những người bình thường quanh bạn. Vì vậy, có thể kết luận được rằng câu trích dẫn ban đầu thực sự hướng đến các sinh viên trẻ tuổi, vì vậy nó chẳng qua có thể chỉ phản ánh một nỗ lực nhằm khuyến khích các sinh viên trẻ luôn kiên trì bất chấp những khó khăn mà họ cảm thấy được.
Ý kiến tiếp theo được nêu lên bởi nhà vật lý học. Einstein đã chứng kiến sự kết thúc của những gì có thể được coi là "vật lý trực quan" của thế kỉ 19 và trước đó. Điều này phần lớn là lỗi của chính ông. Vào năm 1905 (năm "kì diệu" của Einstein), ông đã giới thiệu cho thế giới về cả cơ học lượng tử và thuyết tương đối hẹp. Cho đến thời điểm trước đó (hầu hết) của vật lý hiện đại là thứ có thể dễ dàng hình dung và cảm nhận bằng trực giác.
Vật lý học đã thật sự bắt đầu với những sáng tạo về khối lượng, lực và hệ quán tính. Các khái niệm này là những sáng tạo tự do. Chúng dẫn đến sự hình thành của tư duy cơ học. Đối với một nhà vật lý vào đầu thế kỷ thứ mười chín, hiện thực của thế giới bên ngoài chỉ bao gồm các phần tử và những lực tương tác đơn giản giữa chúng, các lực này chỉ tùy thuộc vào khoảng cách. Ông ta luôn cố gắng giữ càng lâu càng tốt niềm tin rằng ông ta luôn thành công trong việc giải thích được tất cả các sự kiện trong tự nhiên với những khái niệm hiện thực cơ bản này.
Mãi đến khi những khó khăn liên quan đến sự lệch của kim nam châm, liên quan đến cấu trúc của ether đã làm chúng ta phải sáng tạo một hiện thực tinh tế hơn. Sự khám phá hết sức quan trọng về trường điện từ xuất hiện. Tuy vậy, với sự tưởng tượng phong phú đầy sáng tạo và táo bạo trong khoa học, chúng ta vẫn có thể mô hình hóa điện trường và từ trường bằng các đường vẽ trực quan.
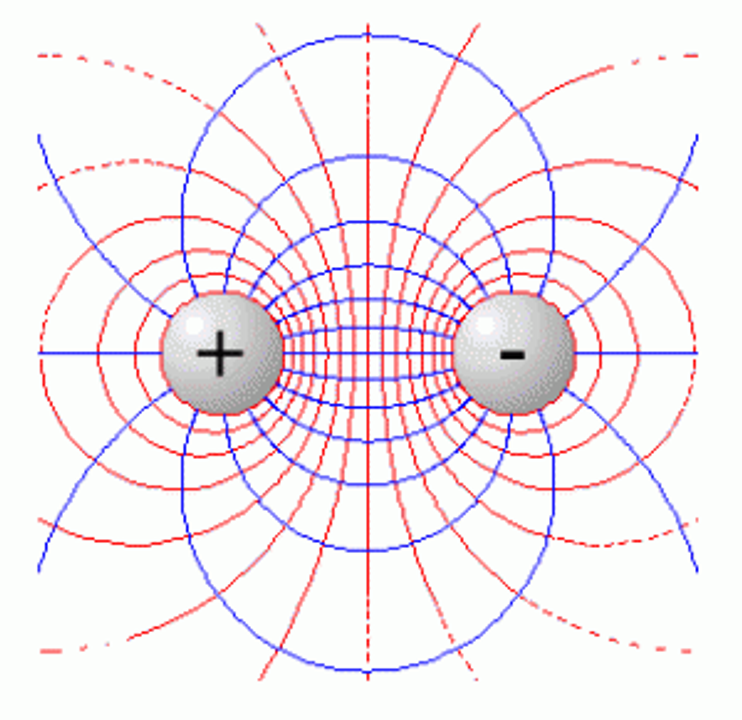
Chúng ta rất dễ hình dung đường sức điện trường (màu xanh)
Hơn nữa, thứ toán học được sử dụng trong đó khá đơn giản. Như kiểu toán đơn giản ta học ở trung học. Với sự ra đời của thuyết tương đối và cơ học lượng tử nhằm bác bỏ những khái niệm cũ và tạo nên những khái niệm mới. Một thời đại của khoa học đã đến, ở đó những kết luận đạt được rơi tuột hoàn toàn ra khỏi sự kiểm soát của toán học truyền thống. Ngày này, trực giác không chỉ trở thành hoàn toàn vô dụng, mà nó sẽ thường xuyên chủ động dẫn dắt bạn đi sai đường nhiều hơn là đúng hướng.
Một số điều đầu tiên chúng ta học được về thuyết tương đối và cơ học lượng tử là: không có khái niệm "hiện tại" đối với hai điểm khác nhau, các hạt thực sự là các sóng, những sóng đó lại thực sự là các hạt, đi nhanh làm cho thời gian chậm lại, đi nhanh làm cho độ dài ngắn đi, năng lượng và vật chất chẳng qua là một, không gian và thời gian gần như giống nhau, đôi khi một số thứ sẽ đột nhiên xuất hiện ở phía bên kia của các rào cản mà chúng không thể vượt qua..vv.. Không có thứ gì trong số khái niệm này có thể dự đoán bằng trực giác và nhiều thứ trong số đó là kết quả của một số kiến thức và phép toán khá phức tạp.
Một nhánh của vật lý được nghiên cứu hiện nay (mô hình chuẩn, lý thuyết dây, và những thứ khác) sử dụng toán học khó đến mức bạn phải mất nhiều năm bồi dưỡng về toán trước khi có thể bắt đầu nắm bắt những gì đang xảy ra. Einstein đã có nhiều năm được đào tạo về toán, nhưng có lẽ không thể tưởng tượng được sự đa dạng rộng lớn của các loại toán học khác nhau cần được vận dụng vì lý thuyết của ông.
Chính bước nhảy vọt cuối cùng này về độ phức tạp trong toán học làm quật ngã Einstein. Tuy nhiên, ngay cả những người mà bạn cho là thông minh một cách không thể tưởng tượng được, hầu như sẽ luôn luôn bị ceh khuất bởi một người thông minh hơn. Mặc dù Einstein có nền tảng vật lý vững chắc, nhưng phải cần tới các nhà toán học (với kiến thức toán và gọng kính dày cộp của họ) mới có thể đưa môn khoa học này tiến lên phía trước.
Một nhà vật lý học chui từ đâu đến khác cho hay. Trong khoảng thời gian từ khi công bố thuyết tương đối hẹp đến khi công bố thuyết tương đối rộng, ông đã dành thời gian tìm hiểu hình học vi phân đủ để phát triển ý tưởng của mình. Đối với Einstein việc này hiển nhiên không hề dễ dàng và cần nhiều tư vấn với những người khác ở Châu Âu. Chẳng hạn, Einstein và Levi-Civita thường xuyên liên lạc với nhau. Vì vậy, ông ấy (ở đây là Levi-Civita) có thể đã trả lời nhận xét của ai đó giống như khi chúng ta nghe thấy rằng bạn bè của ta đang có một thời gian khó khăn với môn toán.

Nhà toán học người Ý Tullio Levi-Civita
Bản thân Einstein và những người đường thời nói gì? Câu trích dẫn sau đây của Einstein có thể giúp chúng ta có thêm một góc nhìn:
"Từ khi các nhà toán học đổ bộ vào thuyết tương đối, tôi không còn hiểu được nó nữa"(A.Sommerfeld "To Albert Einstein’s Seventieth Birthday)
Có khả năng Einstein đã nói điều này vào một lúc nào đó khoảng giữa năm 1907 (khi Minkowski giảng bài về cách phát biểu lại thuyết tương đối hẹp) và năm 1912 (khi Einstein nhận ra rằng ông cần một cách tiếp cận hình học để xây dựng thuyết tương đối rộng). Các nhận xét khác cũng được lưu lại trong khoảng thời gian này bao gồm nhận xét của Einstein trong một bài giảng, khi ông cần rút ra một kết quả cụ thể:
"Điều này đã được thực hiện một cách tao nhã bởi Minkowski; nhưng viên phấn thì rẻ hơn chất xám, và chúng ta sẽ làm điều đó một cách tùy biến mà không gò bó"(Thuật lại bởi Polya trong cuốn Littlewood’s Miscellany)
Sau đó, Eintein nhận ra rằng thuyết tương đối rộng có thể không chỉ yêu cầu những khái niệm này mà còn cần những mở rộng cao cấp hơn của những khái niệm đó:
"Vấn đề này không giải quyết được đối với tôi cho đến năm 1912, khi tôi đột nhiên nhận ra rằng lý thuyết mặt của Gauss nắm giữ chìa khóa để giải mã bí ẩn này. Tôi nhận ra rằng tọa độ bề mặt của Gauss có một ý nghĩa sâu sắc. Tuy nhiên, lúc đó tôi không biết rằng Reimann đã nghiên cứu cơ sở của hình học một cách sâu sắc hơn nữa. Tôi chợt nhận ra rằng lý thuyết của Gauss có trong khóa học hình học do Geiser đưa ra khi tôi còn là sinh viên....
Tôi nhận ra rằng nền tảng hình học có ý nghĩa vật lý. Người bạn thân của tôi, nhà toán học Grossmann đã ở đó khi tôi từ Praha trở về Zurich. Từ ông ấy, lần đầu tiên tôi biết về Ricci và sau đó là Reimann. Vì vậy tôi đã hỏi bạn tôi rằng liệu vấn đề của tôi có thể được giải quyết bằng lý thuyết Reimann hay không, cụ thể là liệu các bất biến của yếu tố đường có thể xác định hoàn toàn các đại lượng mà tôi đang tìm kiếm hay không."
(Einstein, Bài giảng Kyoto, 1922)

Nhà toán học Marcel Grossmann (trái) và nhà vật lý lý thuyết Albert Einstein (phải)
Sau khi tạo ra được những sự liên hệ này vào năm 1912, Einstein không còn lựa chọn nào khác ngoài việc học hình cao cấp mà ông còn thiếu - chủ yếu từ Grossmann. Khi đã thực hiện được như vậy, ông có thể sử dụng hình học cao cấp để phát biểu thuyết tương đối rộng.
Sau này, David Hilbert có tâm sự với người viết tiểu sử của mình:
"Mọi cậu học trò trên những con phố của thủ đô toán học này [Gottingen] đều hiểu về hình học bốn chiều tốt hơn Einstien. Tuy nhiên, bất chấp điều này, Einstein đã làm được việc, chứ không phải các nhà toán học"(Constance Reid, Hilbert, Springer,1996)
Đây quả là một tuyên bố hào phóng của Hilbert, vì ông suýt đánh bại được Einstein trong cuộc chạy đua cuối cùng đến các phương trình trường của thuyết tương đối rộng. Nhưng ông nhận ra rằng tài năng vật lý của Einstein đã cho phép ông ấy làm được nhiều thứ hơn việc bù đắp những sự thiếu hụt của mình về các tinh tế toán học.

Nguồn:
[1] Cuốn "Sự tiến hóa vật lý" - Albert Einstein, Leopold Infeld
[2] Cuốn "Albert Einstein: philosopher-scientist" - Paul A. Schilpp
[3] Cuốn Littlewood, J. E. (1986), Bollobás, Béla (ed.), Littlewood’s miscellany, Cambridge: Cambridge University Press.
Đọc thêm:

Quan điểm - Tranh luận
/quan-diem-tranh-luan
Bài viết nổi bật khác
- Hot nhất
- Mới nhất