Sau những bài viết linh tinh về nhiều chủ đề, mình muốn thử sức viết một bài về chuyên ngành mình đang học để thử sức xem sao. Mục tiêu của mình trong những bài viết thuộc series này đó chính là làm sao cho Vật lý, vốn là một môn học nhiều người cho là khô khan, trở thành một thứ gì đó thực sự rất kì diệu, thú vị và dễ hiểu (cái này thì hên xui.) Chính vì vậy, mình sẽ cố gắng hạn chế sử dụng những ký hiệu toán học nhất có thể và tập trung vào giải thích ý tưởng đằng sau thứ Vật lý mà mình đang nói đến.
Bài viết được dựa trên những kiến thức mình được học ở trên trường và những kiến thức mình tự tìm tòi. Đến hiện tại, mình vẫn đang chỉ ở trình độ Vật lý đại học nên có thể sẽ vẫn còn một vài sai sót về mặt kiến thức, mong mọi người thông cảm!

Nhà toán học Emmy Noether (1882 - 1935)
Lí do vì sao mình để hình bà làm thumbnail thì các bạn đọc tới cuối series sẽ rõ! (Hoặc các bạn có thể tự search trước ^^)
PHẦN 1: Giới thiệu về đối xứng
Chắc hẳn mọi người cũng đều ít nhiều hiểu được "sự đối xứng" là gì. Từ "đối xứng" trong đời sống hằng ngày được dùng đề chỉ một vật gì đó nhìn cân đối, tạo ra một cảm giác hài hòa cho người nhìn. Sự đối xứng thường được con người để ví tới một thứ gì đó đẹp đẽ, tích cực.
Anh ấy/cô ấy có một khuôn mặt đối xứng!
Sự đối xứng còn có thể được tìm thấy rất nhiều trong thiên nhiên, trong những bông hoa, chiếc lá, cây cối, thú rừng, vân vân và mây mây. Sự đối xứng dường như là một phần không thể thiếu của tự nhiên.

Hoa Drosophyllum. (Nguồn: flickr / ramamayoor) lấy từ bài báo của VietnamPlus
Thế vật lý dùng để làm gì? Đối với mình mà nói, Vật lý là một môn học mà ta sử dụng công cụ là toán để miêu tả lại tự nhiên và sử dụng nó để dự đoán và tính toán những điều sẽ xảy ra và có thể xảy ra.
Vậy thì nếu sự đối xứng là một phần của thiên nhiên và vũ trụ, thì ta hoàn toàn có thể ứng dụng nó vào Vật lý đúng chứ? Chính xác là như vậy! Trong Toán học và Vật lý có một định nghĩa rất chi là cụ thể cho "sự đối xứng."
Một sự biến đổi đối với một vật mà khiến vật thể đó không thay đổiThì là một đối xứng
Ví dụ, giả sử ta có một con bướm như ở hình dưới:
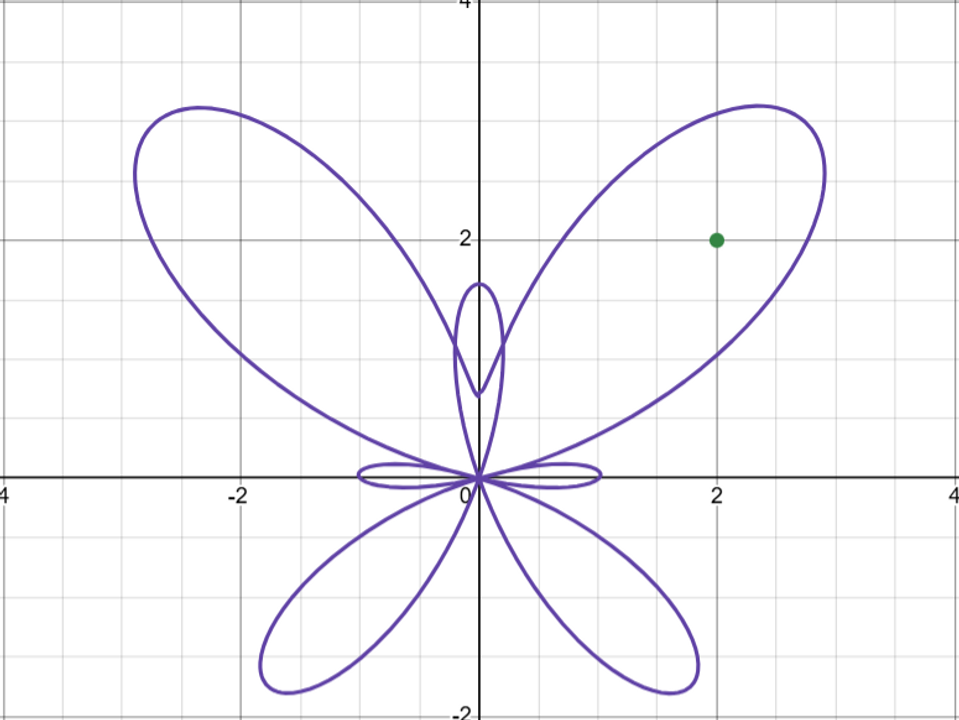
Hình ảnh một con bướm được tạo bằng Desmos và mình có cho thêm điểm A(2,2) ở bên phải để tham khảo sự khác biệt
Mình sẽ phản chiếu hình này lại bằng phần mềm qua trục dọc, ta sẽ có hình như sau:
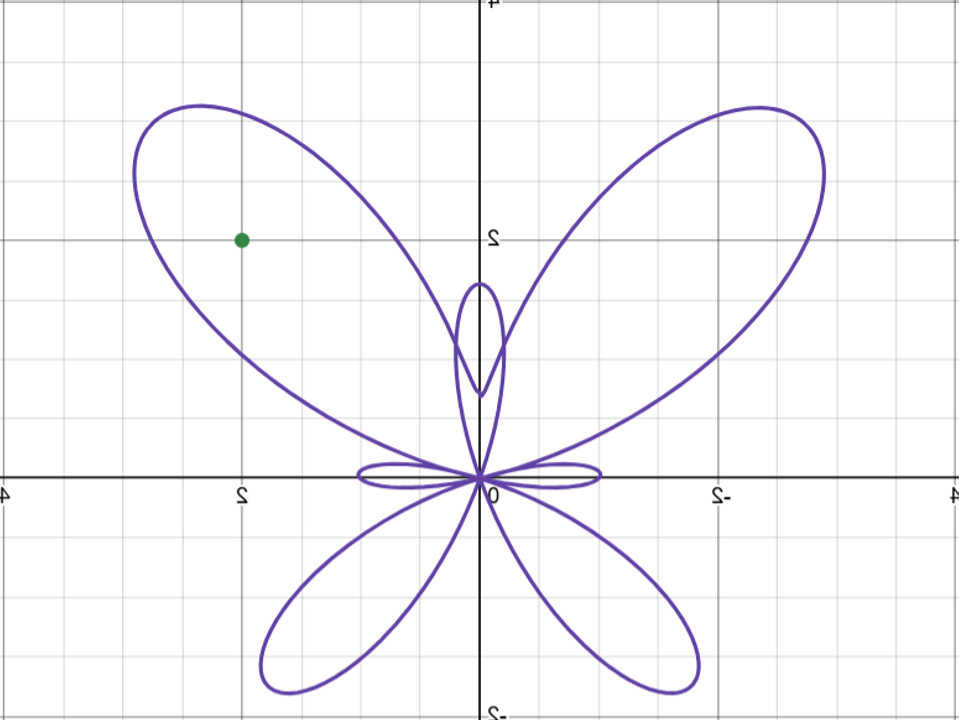
Hình con bướm được phản chiếu qua trục dọc, điểm tham khảo giờ đã chuyển sang vị trí bên trái
Như ta có thể thấy, hình ảnh con bướm đã bị lật ngược, song, nếu không phải vì các con số ở trong ảnh và điểm tham khảo, ta sẽ không tài nào có thể biết được rằng con bướm đã bị biến đổi cả. Từ đó, ta có thể kết luận rằng "sự phản chiếu qua trục dọc" là một đối xứng của con bướm.
Tất nhiên, đây không phải là sự đối xứng duy nhất tồn tại trong tự nhiên và vũ trụ. Mình sẽ cố gắng giới thiệu thêm nhiều cái đối xứng nữa và những sự thật về vũ trụ mà chúng bóc tách.
Sự đối xứng cũng không nhất thiết chỉ là một sự biến đổi duy nhất, mà còn có thể là một tổ hợp của nhiều sự biến đổi. Để lấy ví dụ, hãy tưởng tượng ta có một bàn cờ vua vô hạn.

Một bàn cờ vua vô hạn về hai phương ngang và thẳng đứng
Vì bàn cờ vua là vô hạn, thế tức là nếu ta dịch chuyển toàn bộ bàn cờ sang phải một ô, rồi tiếp tục dịch chuyển bàn cờ xuống một ô, ta sẽ có được bàn cờ vua ban đầu. Từ đó, ta kết luận "sự dịch chuyển sang phải một ô + sự dịch chuyển xuống dưới một ô" chính là một đối xứng của bàn cờ vô hạn nói trên!
Và phải cảm ơn trời vì chúng ta có thể ứng dụng sự đối xứng vào trong Toán học và Vật lý. Nếu bạn đã học Vật lý vào thời cấp 2, cấp 3 thì chắc cũng biết rằng chỉ bằng việc lý luận đối xứng, chúng ta thể giảm được khối lượng tính toán đi một nửa, thậm chí một phần tư. Và tin mình đi, càng học Vật lý bậc cao hơn thì đối xứng càng hữu dụng (mình đã chết lên chết xuống với thuyết tương đối rộng.)
Để lấy ví dụ, mình có một bài toán về tính toán lực căng dây ở dưới (mình sẽ không đi sâu vào giải bài toán đâu nên đừng lo):
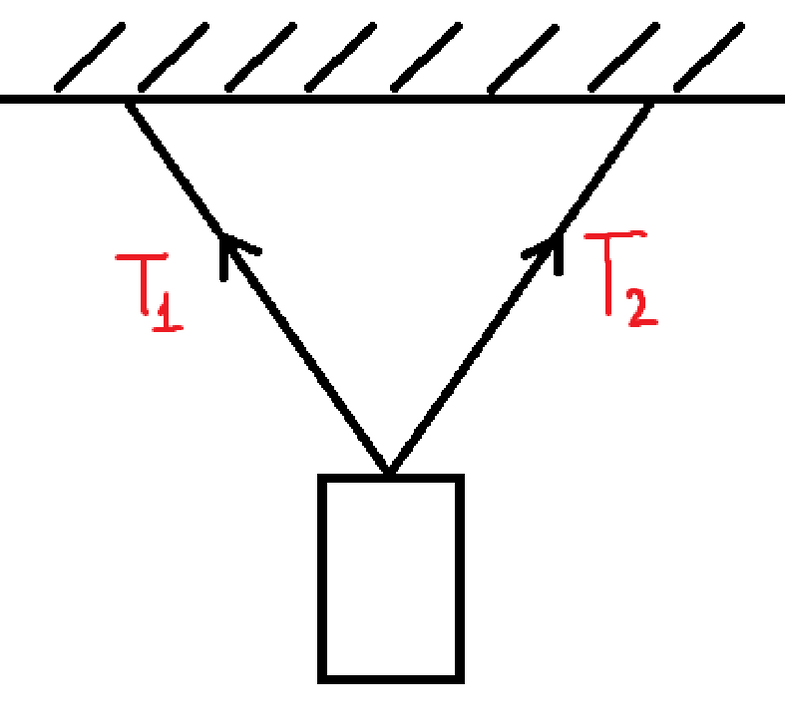
Hai sợi dây đối xứng với nhau được gắn với một vật để treo vật đó lên.
Đề bài: Ta cần tính lực căng dây (lực kéo) của hai sợi dây
Vì ta biết dây 1 và dây 2 đối xứng với nhau, ta có thể dự đoán rằng lực căng dây của chúng sẽ bằng nhau và ta chỉ cần quan tâm đến việc tính toán lực căng của một dây mà thôi!
Giờ chúng ta đã có nền tảng chung cho sự đối xứng rồi, hãy cùng tiến tới những thứ thú vị hơn nhé!
PHẦN 2: Nguyên lý của Marie về sự đối xứng
Người ta thường hay nhắc về Marie Curie mà bỏ qua người chồng của bà Pierre Currie, cũng là một nhà Vật lý học và Hóa học xuất chúng. Ông là một người khởi xướng lĩnh vực nghiên cứu về sự đối xứng trong Vật lý.

Hình ảnh của Pierre Curie, chồng của Marie Curie
Khi đang nghiên cứu về từ tính và vật liệu, ông đã quan sát được một vài điều vô cùng thú vị về sự đối xứng. Ông đã để ý rằng trong một mạng tinh thể lập phương (một cách các nguyên tử/phân tử sắp xếp bên trong một tinh thể) có rất nhiều sự đối xứng, bao gồm đối xứng trục dọc, đối xứng quay 90 độ và vân vân.
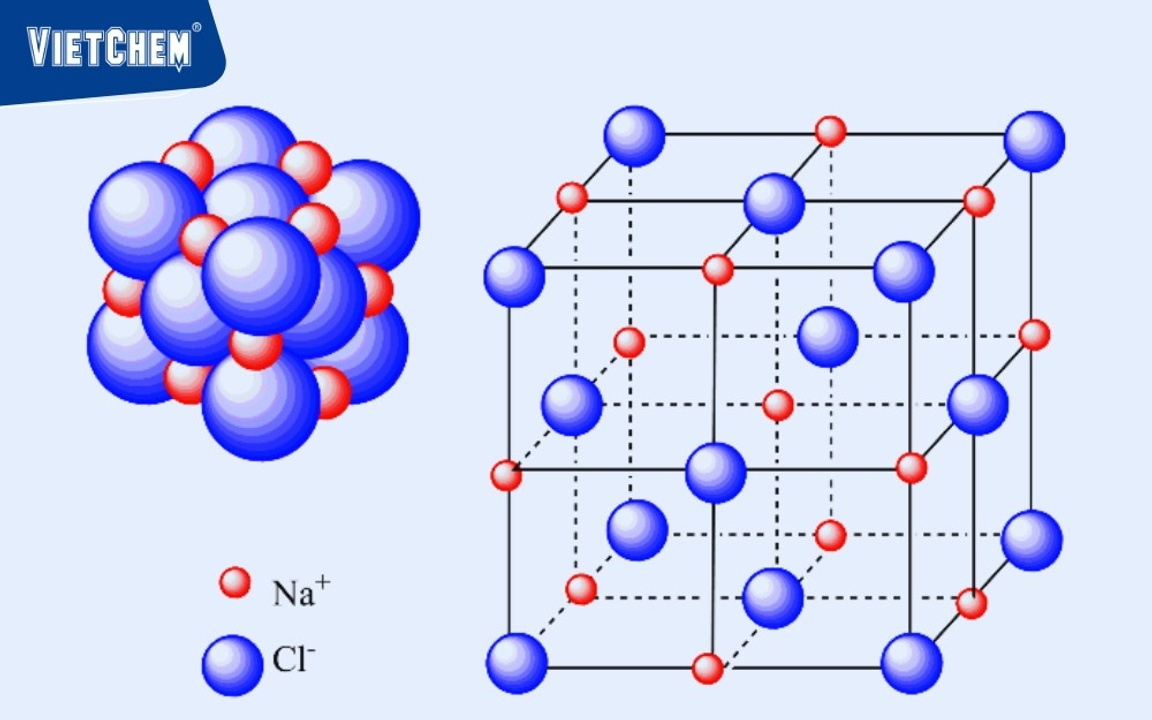
Minh họa về mạng tinh thể lập phương với các ion Na và Cl
Thế tức là nếu tinh thể mà ông đang nghiên cứu có tính dẫn điện, thì việc biến đổi quay 90 độ khiến vật liệu sẽ giữ nguyên tính chất vốn có của nó. Điều này có nghĩa là tính dẫn điện hẳn cũng có đối xứng nào đó tương ứng với sự đối xứng nói trên của mạng tinh thể.
Ông đưa ra suy đoán,
Nếu một nguyên nhân (một hiện tượng) tạo ra một kết quả nào đó, thì kết quả cũng sẽ có một sự đối xứng tương ứng với sự đối xứng của nguyên nhân.
Về sau, người ta gọi đó là nguyên lý của Curie. Tất nhiên, đây không phải một nguyên lý được chứng minh một cách kĩ lưỡng nên tại thời điểm đó, có rất nhiều chỉ trích tới nguyên lý của ông. Có người nói rằng nó vô nghĩa, chả khác gì nói rằng vì "đối xứng" nên ta suy ra "đối xứng. Tuy vậy, nó vẫn là một nguyên lý vô cùng hữu dụng để chứng minh nhiều thứ nên ta hãy tạm thời công nhận nguyên lý này.
Vậy đâu là nguyên nhân của toàn bộ vũ trụ? Chính là các định luật Vật lý! Toàn bộ sự vật trên vũ trụ này đều phải tuân theo các định luật Vật lý. Vậy nếu bản thân các định luật Vật lý có những sự đối xứng thì sao?
Hãy tưởng tượng một vũ trụ khác mà tất cả các định luật Vật lý được biến đổi bằng một đối xứng, điều đó có nghĩa là các kết quả của vũ trụ đó sẽ phải giống y hệt chúng ta. Nói theo cách khác, ta đã bảo toàn được vũ trụ.
Nói theo cách khác (một lần nữa), nếu ta nắm bắt được tất cả các đối xứng của các định luật Vật lý, ta sẽ có một công cụ cực kì hữu dụng để giải mã được toàn bộ vũ trụ vì ta luôn có thể chọn cái "vũ trụ khác" mà để thuận tiện cho ta nhất!
P/S: Bật mí trước, các đối xứng của định luật Vật lý không chỉ đơn giản là phản chiếu, xoay xoay các thứ đâu!
Còn tiếp...
Kết phần 1
Cảm ơn mọi người đã đọc đến đây, với bài viết đầu tiên này mục tiêu của mình chỉ mới là khơi dậy sự hứng thú của người đọc về sự đối xứng nên cũng chưa nhắc gì nhiều đến Vật lý. Mong rằng mình đã đạt được điều đó.
Mình sẽ cố gắng tiếp tục series này nhưng chắc cũng sẽ phải mất kha khá thời gian vì hiện tại mình vẫn là sinh viên và phải cân bằng giữa học và làm. Mong mọi người vẫn sẽ tiếp tục theo dõi!
Reference & Resources
Tinkerin' Thinkers. (2011, January 28). Richard Feynman - The Character of Physical Law - Part4 Symmetry in Physical Law (full version). YouTube. https://www.youtube.com/watch?v=zQ6o1cDxV7o
Chalmers, A. F. (1970). Curie’s Principle. The British Journal for the Philosophy of Science, 21(2), 133–148. http://www.jstor.org/stable/686695
Và một vài tài liệu nội bộ của trường mình nên không thể tiết lộ =(

Khoa học - Công nghệ
/khoa-hoc-cong-nghe
Bài viết nổi bật khác
- Hot nhất
- Mới nhất