Chuyện về một dòng họ toán học: Gia đình Bernoulli
Qua lịch sử văn hóa loài người, đã có những gia đình đóng góp đáng kể cho xã hội nhiều thế hệ liên tiếp các nhà khoa học, văn nghệ...
Lời nói đầu
Qua lịch sử văn hóa loài người, đã có những gia đình đóng góp đáng kể cho xã hội nhiều thế hệ liên tiếp các nhà khoa học, văn nghệ sĩ nổi tiếng. Trong số các gia đình vinh quang đó có gia đình họ Bernoulli.
Bernoulli là một gia tộc có truyền thống làm khoa học với rất nhiều công trình quan trọng để đời. Nhiều tài liệu vì không hay ghi rõ tên đầy đủ mà chỉ có mỗi Bernoulli nên có thể khiến cho một số người không hay rằng tồn tại một gia tộc độc nhất trong lịch sử, chưa từng có trước đây và có thể sẽ chẳng bao giờ xuất hiện một gia tộc giống như vậy.
Trong khoảng thời gian giữa thế kỷ 17 đến giữa thế kỷ 19, gia tộc này đã cho ra đời tám nhà toán học xuất chúng. Họ không chỉ nổi tiếng vì những thành quả trong toán học mà còn nổi tiếng về sự đấu đá, thù ghét nội bộ nhằm giành giật địa vị cao hơn trong ngành toán. Nói riêng, cây gia phả nhà Bernoulli còn sinh ra những nhân vật tầm cỡ khác sau này gồm Pierre Curie, nhà vật lý, hoá học nổi tiếng với người vợ Marie Curie.

Nguồn: Mathtasy Toán học kì thú
Nguồn gốc
Dòng họ Bernoulli có nguồn gốc từ Hà Lan, theo đạo Tin Lành nhánh Calvinism (nhánh Tin Lành Calvinism do John Calvin (1509–1664) thành lập tách khỏi ảnh hưởng của Thiên Chúa giáo La Mã).
Năm 1567, vua Philip của Tây Ban Nha đã gửi một đạo quân hùng mạnh đi trừng phạt những xứ nào chống lại vua chúa Tây Ban Nha, chống lại Thiên Chúa giáo La Mã, thiết lập lại uy quyền. Trước sự đe dọa ấy, gia đình Bernoulli chạy trốn qua Basel, Thụy Sĩ. Khi ấy Thụy Sĩ là một xứ thương mại giàu có nhất ở Trung Âu.

Basel, Thụy Sĩ
Bernoulli đầu tiên sinh ra tại Basel là Nicolas Bernoulli (1623–1708) thương gia thành đạt ở phố Basel và ông có bốn người con trai là Jacob I, Nicolas, Johann I và Hieronymous I. Các chữ số La Mã “I” phản ánh một thực tế hay cũng có thể coi là một vấn đề rằng nhiều hậu duệ đời sau thường lấy lại tên của cha hoặc chú của mình.
Mặc dù ông Nicolas không có biểu hiện nào về năng khiếu Toán học, nhưng các thế hệ con cháu của ông về sau hầu hết là những nhà Toán học tài năng, trong số đó có những người tầm cỡ hàng đầu châu Âu thời ấy: Jacob Bernoulli, Johann Bernoulli và Daniel Berboulli.

Nguồn: Cantor's Paradise
Có thể nói cùng với Isaac Newton, Gottfried Leibniz, Leonhard Euler, và Joseph Lagrange, ba nhà Toán học Bernoulli kể trên đã đóng góp, phát triển, định hình các lĩnh vực Tính vi-Tích - phân, Hình học, Cơ học, Nhiệt động học (Thermodynamics), Thủy động học (Hydrodynamics), Quang học, Thiên văn học, Xác suất học trong suốt thế kỷ 17 và 18.
1. Jacob Bernoulli

Jacob Bernoulli (27 tháng 12 năm 1654 – 16 tháng 8 năm 1705) là con trai lớn nhất của Nicolas Bernoulli, được xem như là một trong số những nhà Toán học có ảnh hưởng rất lớn thời bấy giờ mặc dù xuất thân từ một gia đình không có truyền thống Toán học hoặc Khoa học.
Cha mẹ buộc ông phải học Triết học và Thần học, những môn không thể thiếu để trở thành một người thượng lưu thành đạt của xã hội thời ấy. Jacob đành phải dốc hết sức học các môn thần học và tiếng nước ngoài. Nhưng ông vẫn không thể bỏ được toán học và thường xuyên giấu cha để học toán.
Năm mười bảy tuổi, Jacob đã giải được những bài toán phức tạp như tính lịch, tính quỹ đạo của sao Chổi . . vv . . Tài năng của ông khi ấy càng ngày càng bộc lộ rõ rệt. Ông tốt nghiệp Thần học năm 1676, sau đó rời bỏ gia đình lên Geneva (Thụy Sĩ) làm chân giáo viên dạy kèm Toán học và Khoa học để kiếm sống.
Một thời gian ngắn sau đó, ông qua Pháp, ở đó trong hai năm theo học Toán với những người theo trường phái Descartes. Năm 1681, ông sang Hà Lan, rồi từ đó tới Anh. Tại London, ông gặp gỡ một số nhà Toán học và Khoa học nổi tiếng trong đó có Robert Hooke (1635 – 1703), Robert Boyle (1627 –1691). Ông vẫn giữ mối liên lạc trong nhiều năm sau qua thư tín. Qua những chuyến đi đó đây để học hỏi, ông đã định hướng hẳn cho mình hai lĩnh vực chính, đó là Toán học và Thiên văn học. Năm 1683, ông trở về lại Thụy Sĩ và xin được chân giảng dạy Toán - Cơ tại Đại học Basel, mặc dù gia đình ông phản đối.

Trường Đại học Basel, Thụy Sĩ
Trong khoảng thời gian từ năm 1682 tới 1704, Jacob Bernoulli đã công bố năm tác phẩm về chuỗi số vô tận, trong đó ông đưa ra nhiều kết quả quan trọng. Thí dụ ông chứng minh được chuỗi số điều hòa

(1)
là phân kỳ. Thật ra kết quả này đã được nhà Toán học Ý Pietro Mengoli (1626 – 1686) chứng minh khoảng 40 năm trước.
Ngoài ra, Jacob còn chứng minh được chuỗi số
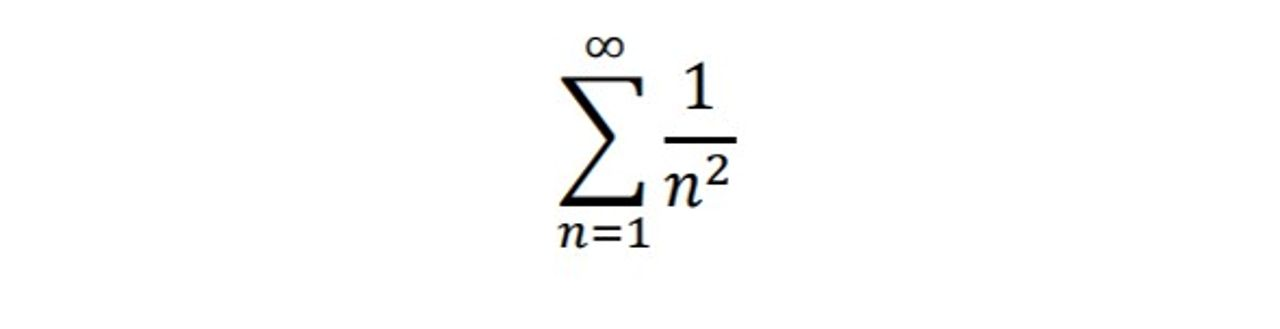
(2)
là hội tụ. Ông đã chứng minh được tổng số này nhỏ hơn 2, tuy vậy ông không tìm được giá trị của tổng số.
Bài toán này khó đến nỗi ngay cả Jacob Bernoulli sau khi đã vận hết mười hai thành công lực mà vẫn thất bại mà phải thốt lên rằng:
Tôi đã cố gắng nhiều lắm mà vẫn không tìm ra. Ai tìm được và cho tôi biết thì tôi xin cảm ơn vô cùng.
Phải mất khoảng 30 năm sau, năm 1734, nhà toán học vĩ đại Leonhard Euler khi ấy chỉ mới hai mươi ba tuổi đã giải quyết vấn đề trên vô cùng độc đáo, ấn tượng đến kì lạ được tổng này bằng:
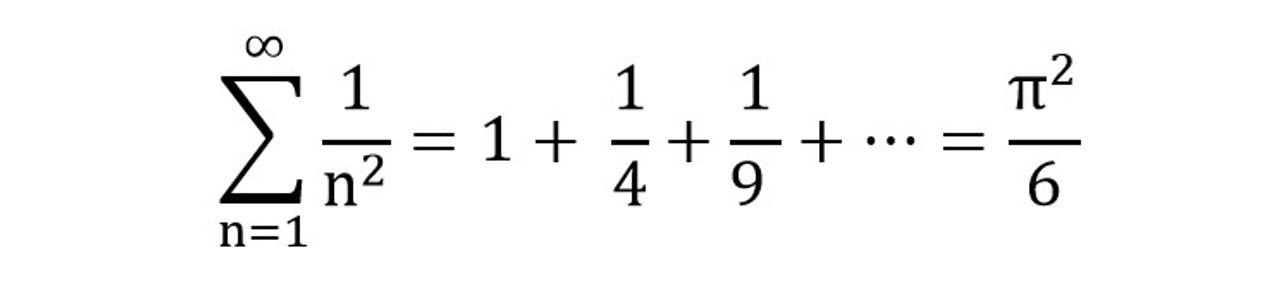
(3)
Tháng 5 năm 1690, ông cho công bố một bài báo quan trọng về đường đẳng thời (Isochrone hay tautochrone curve) trên tờ Acta Eruditorum, tờ báo uy tín được thành lập từ năm 1682 do chính Leibniz làm chủ bút đầu tiên.
Về khái niệm, đường đẳng thời là đường cong đi xuống, trên đó mọi chất điểm chỉ dưới tác dụng của trọng lực, bất kỳ khởi hành ở điểm nào, cũng sẽ đạt điểm đáy trong cùng một thời gian như nhau.
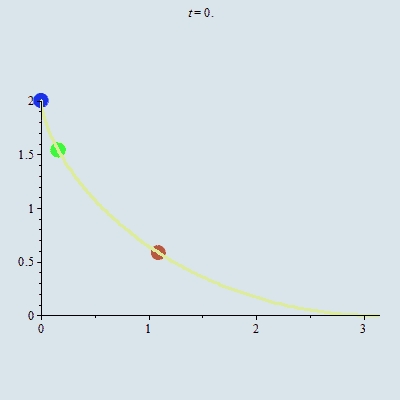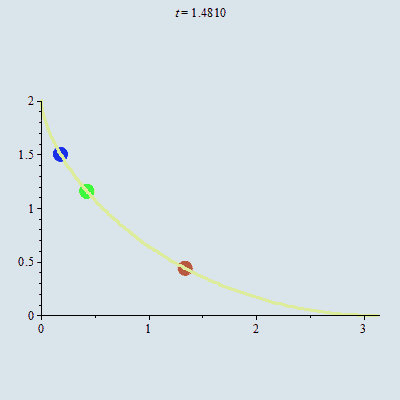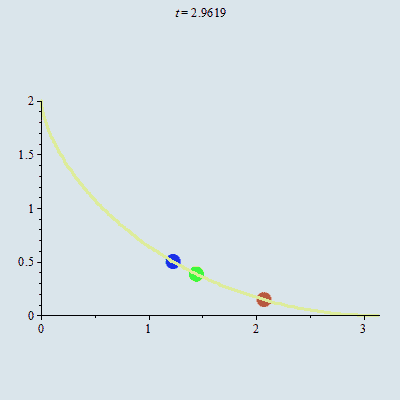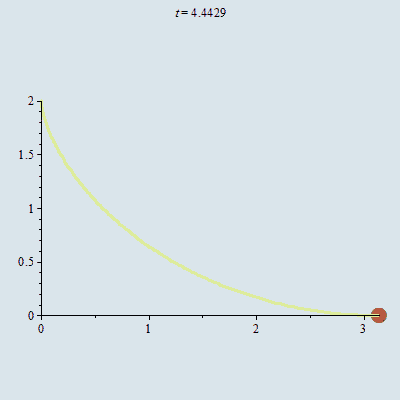
Minh họa về bài toán đường đẳng thời. Nguồn: Blog TOÁN HỌC TƯƠI ĐẸP
Jacob Bernoulli chứng minh được rằng bài toán xác định đường đẳng thời tương đương với bài toán giải một phương trình vi phân bậc nhất tuyến tính.
Bài toán này trước đó đã được Christian Huygens (1629 – 1695) vào năm 1659 giải theo hướng vật lý học (sử dụng con lắc đồng) trong cuốn Horologium Oscillatorium. Nhưng chính Jacob Bernoulli là người đầu tiên dùng đến các phép tính tích phân để giải bài toán này.
Cũng qua bài báo này, Jacob Bernoulli thiết lập và đưa ra phương pháp giải phương trinh vi phân gọi là phương pháp phân ly biến số (method of separation of vari-ables). Đường cong "đẳng thời" có tên gọi là đường cycloid.
Cycloid là quỹ tích những điểm cố định trên một đường tròn cho sẵn khi đường tròn lăn không trượt trên một đường thẳng. Chúng có thể dễ dàng nhận thấy hình ảnh của nó được tạo ra bởi một vòng tròn lăn.

Hình ảnh thực tế đường Cycloid. Nguồn: Wikipedia
Năm 1696, Jacob Bernoulli đưa ra được cách giải bài toán bằng phương trình vi phân dạng:
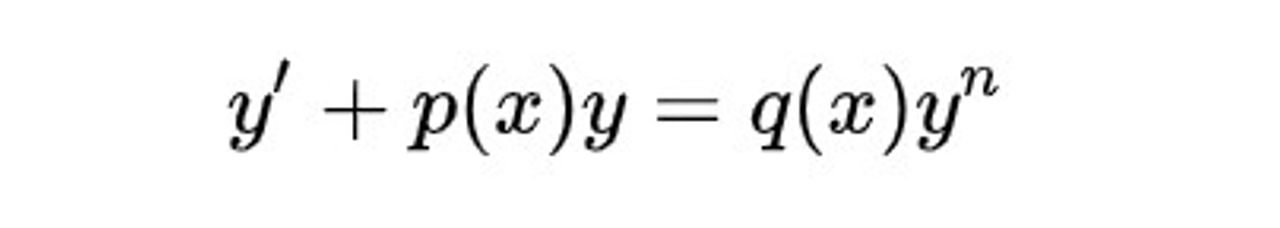
(4)
mà ngày nay chúng ta gọi là phương trình vi phân Bernoulli. Ông đã áp dụng phương trình này để giải nhiều bài toán Hình học và Cơ học khác.
Bây giờ ta nói về đường cong có tên là đường dây xích (Catenary theo tiếng Anh hay Chaˆınette theo tiếng Pháp). Đó là dạng của đường cong của một dây xích treo giữa hai trụ dưới tác dụng của trọng lượng của nó.

Hình ảnh thực tế về đường dây xích
Nhà Toán học và Thiên văn học người Ý Galileo Galilei (1564 – 1642) đã nghĩ đến đường cong này và cho rằng đó là một phần của một parabol.
Năm 1669 nhà toán học người Đức Joachim Jungius đã bác bỏ ý tưởng của Galileo cho rằng đường cong của một chuỗi treo dưới tác dụng lực hấp dẫn sẽ là một parabol. Huygens là người đầu tiên sử dụng tên gọi dây xích trong một bức thư cho Leibniz năm 1690.
Tháng 5 năm 1690, Jacob Bernoulli chính thức đưa bài toán này lên tờ Acta Eruditorum như là một bài toán thách thức:
“Hãy xác định hình dạng đường cong của một sợi dây đồng chất (khối lượng phân phối đều) được treo giữa hai điểm cố định.”
Một năm sau, trong số báo tháng 6 năm 1691, có ba lời giải được công bố: một của Huygens, một của Leibniz và một của Johann Bernoulli, em trai út của Jacob Bernoulli. Cả ba lời giải đều đi tới cùng kết quả nhưng bằng ba cách hoàn toàn khác nhau. Phương trình Descartes của đường cong ấy là:
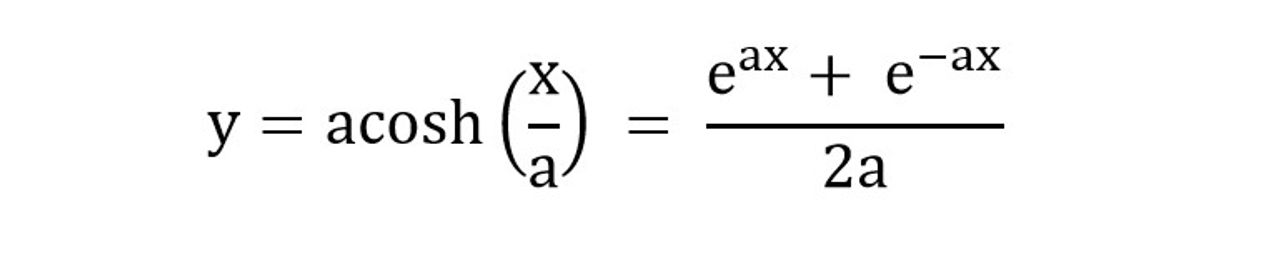
(5)
trong đó cosh là cosin hyperbol, a là hằng số tùy thuộc vào khối lượng và sức căng của sợi dây, a = T/ω, T là phần hợp thành chiều ngang của lực căng dây, ω là trọng lượng của một đơn vị độ dài của dây.
Hình đường cong này rất quan trọng, được thể hiện qua nhiều hiện tượng và nhiều kiến trúc nổi tiếng. Ví dụ, mặt cắt của cánh buồm vuông dưới áp lực của gió sẽ có dạng dây xích (vấn đề này đã được Jacob Bernoulli xem xét). Các vòm có dạng một dây xích ngược (chẳng hạn như Cổng vòm của Saarinen ở St.Louis) thường được sử dụng trong kiến trúc và xây dựng. Chúng có độ ổn định cao vì các lực nén bên trong cân bằng và không gây sụt lún.

Gateway Arch (trái) và những vòm trong trường Đại học Oxford (phái). Đó là những hình có dạng catenary úp ngược.

Vòm nhà thờ Santa Maria del Fiore ở Firenze theo hình dạng catenary úp ngược
Nói thêm bên lề về parabol và catenary, mặc dù parabol và catenary có nét tương đồng về hình dáng ở một mức độ nào đó, nhưng chúng là hai đường cong được xây dựng từ những biểu thức toán học khác nhau.
Parabol thường được sách giáo khoa chú trọng hơn. Việc lựa chọn parabol thay cho dây xích để mô hình hóa các đường cong, chẳng hạn như khi biểu diễn cầu treo hoặc dây cáp là điều khá phổ biến. Lý do là bởi phương trình của parabol đơn giản hơn, dễ xử lý và không đòi hỏi kiến thức chuyên sâu về giải tích hay logarit tự nhiên. Dẫu vậy, cả hai đường cong này đều mang những đặc trưng riêng và có vai trò quan trọng trong các ứng dụng thực tiễn.
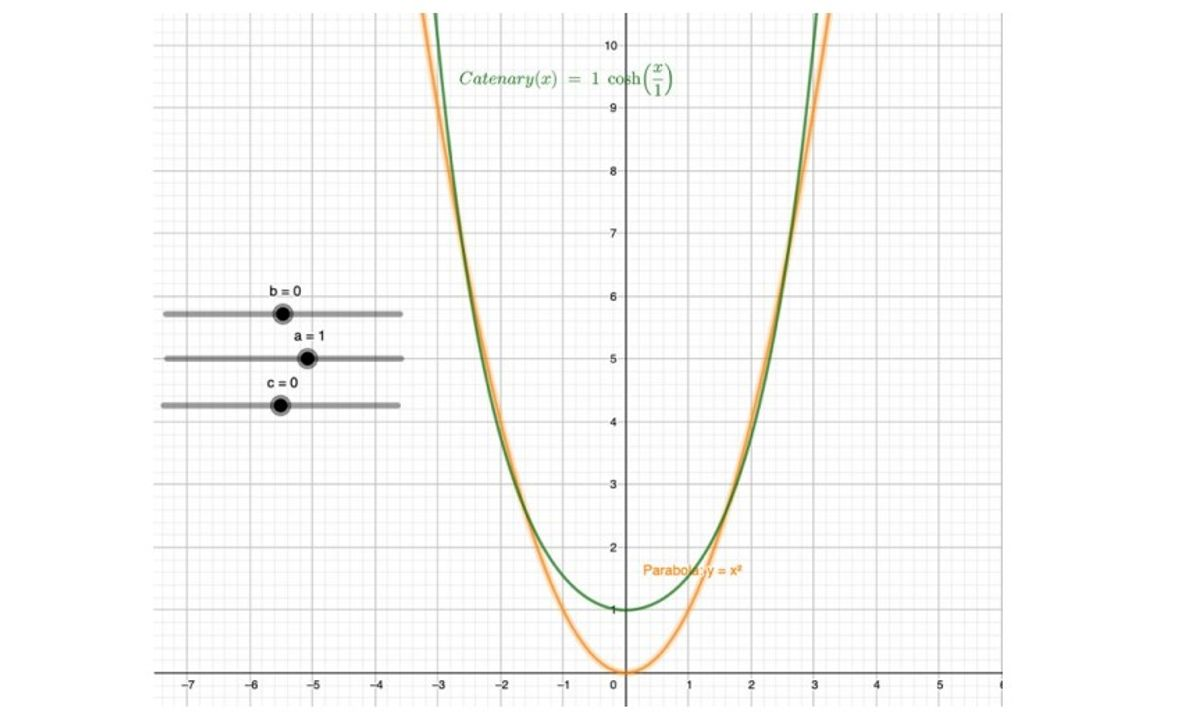
So sánh cơ bản giữa parabol và catenary bằng GeoGebra
Jacob Bernoulli còn là một trong những nhà Toán học tiên phong trong lý thuyết xác suất. Bài báo đầu tiên của ông về xác suất công bố năm 1685. Đóng góp lớn nhất của Jacob Bernoulli là nghiên cứu mang tên Ars Conjectandi (Nghệ thuật suy đoán), tác phẩm này chỉ được công bố năm 1713 sau khi ông mất 6 năm. Cùng với tác phẩm De ratiociniis in ludo aleae (Về các phép tính trong trò chơi may rủi) của Huygens được xem là hai tác phẩm đầu tiên về xác suất.

Ars Conjectandi
Trong cuốn sách, Bernoulli đã tổng hợp và xem xét lại công trình của những nhà toán học khác về xác suất, đặc biệt là công trình của Van Schooten , Leibniz và Prestet. Các số Bernoulli xuất hiện trong cuốn sách trong phần bàn luận về chuỗi lũy thừa (exponential series). Ông trình bày thêm trong sách về các phép tính hoán vị, tổ hợp, chuỗi vô tận, phân bố nhị thức (binomial distribution), định luật về số lớn (Bernoulli law of large numbers). Trong đó ông còn đưa ra nhiều ví dụ về số tiền kỳ vọng mà người chơi có thể thắng trong các trò chơi may rủi khác nhau. Ngoài ra, cuốn sách cũng chứa đựng những suy ngẫm thú vị về bản chất thực sự của xác suất.

Trong Sách chuyên đề toán 12 bộ cánh diều trang 13, các bạn học sinh lớp 12 được học về phân bố nhị thức (binomial distribution).
Ngoài ra, Jacob là người chứng minh được bất đẳng thức Bernoulli thú vị sau đây:
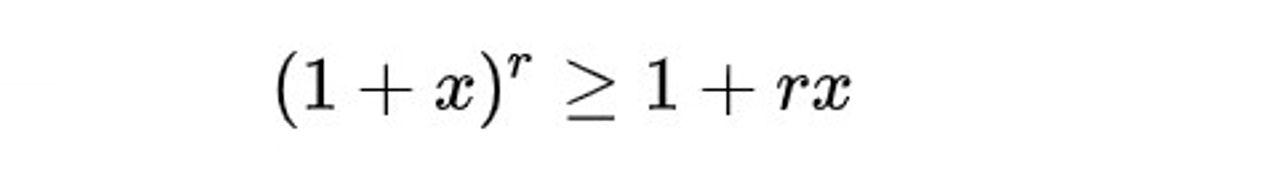
(6)
với mọi số nguyên r ≥ 0 và với mọi số thực x > −1.
Nếu số mũ r là chẵn, thì bất đẳng thức này đúng với mọi số thực x. Bất đẳng thức này trở thành bất đẳng thức nghiêm ngặt như sau:
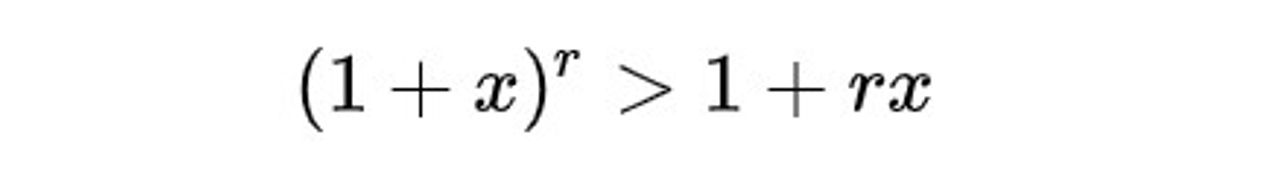
(7)
với mọi số nguyên r ≥ 2 và với mọi số thực x ≥ −1 với x ≠ 0.
Bất đẳng thức Bernoulli thường được dùng trong việc chứng minh các bất đẳng thức khác hoặc trong một vài trường hợp có thể được sử dụng để giải hệ phương trình hai ẩn. Bản thân nó có thể được chứng minh bằng phương pháp quy nạp toán học.
Cũng chính Jacob Bernoulli là người đầu tiên chứng minh được
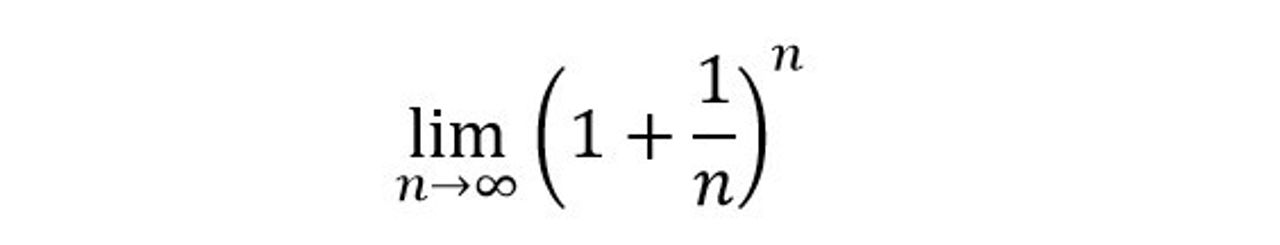
(8)
tồn tại và giá trị của giới hạn nằm giữa số 2 và số 3. Sau này nhà toán học Leonhard Euler xác định được chính xác đó là số e xấp xỉ khoảng 2,71828..., nghĩa là e là giới hạn của một chuỗi số khi số lần cộng thêm vào tiến tới vô cùng.
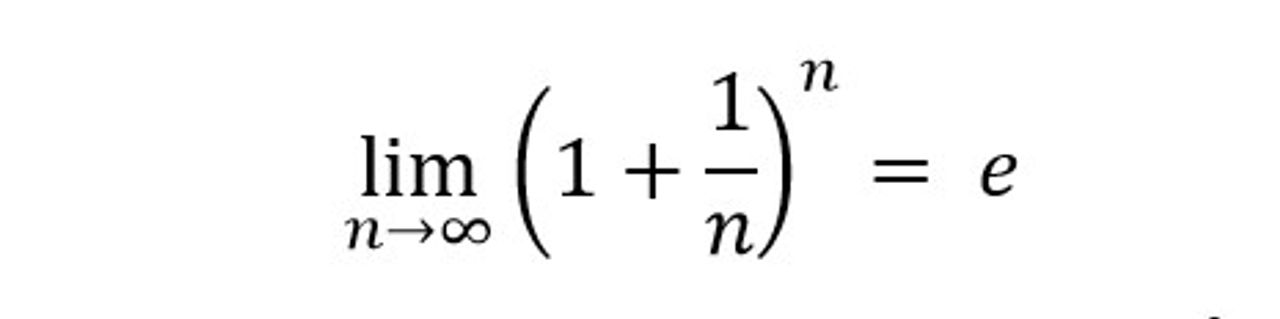
(9)
Hằng số Euler (kí hiệu là e ) là một hằng số toán học quan trọng. Đây là một số vô hạn thập phân và nó không có một biểu diễn chính xác nào dưới dạng phân số. Hằng số Euler đã xuất hiện tự nhiên trong nhiều lĩnh vực khác như bài toán lãi suất kép, phép thử lặp Bernoulli, phân phối chuẩn (Normal distribution), ..vv..
Jacob Bernoulli còn quan tâm một cách thích thú đến những đường xoắn ốc logarithm mà Descartes đã giới thiệu từ năm 1637. Ông gọi nó là Spira mirabilis, "đường xoắn kỳ diệu".
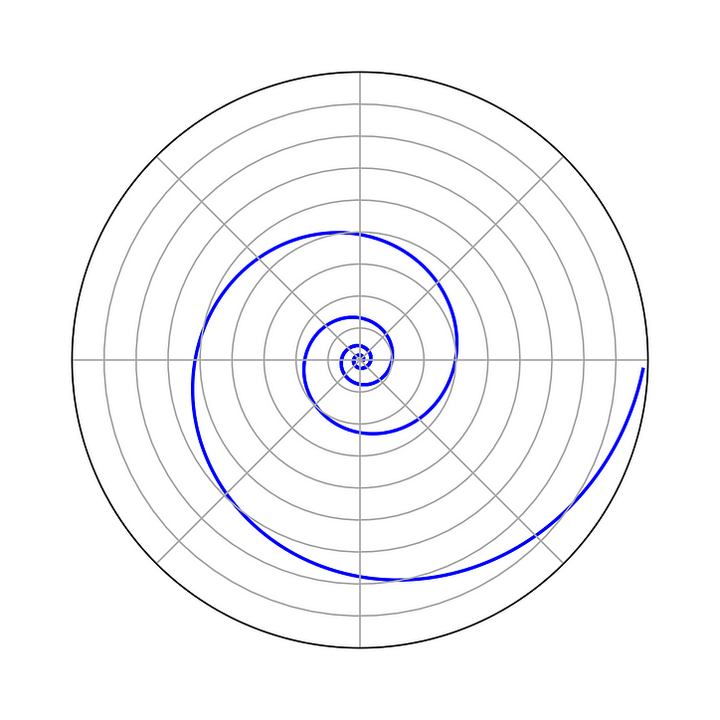
Đường xoắn ốc Logarit
Christopher Wren (1632 - 1723) đã nghiên cứu hình dạng của một vỏ sò để tìm hiểu thêm về nó. Ông phát hiện rằng độ dài các đoạn thẳng nối từ tâm vỏ sò (tức gốc của xoắn ốc) đến các điểm trên vỏ tăng dần, nhưng biên độ của các góc tạo bởi những đoạn thẳng đó với tiếp tuyến tương ứng trên vỏ thì luôn không đổi. Trong khi đó, Jacob Bernoulli lại say mê với tính tự đồng dạng của đường cong này.
Không chỉ các nhà toán học, mà cả các nhà vật lý, sinh học, thiên văn học và khí tượng học cũng đều say mê đường cong ấy. Lý do là bởi hình dạng này xuất hiện rất phổ biến trong tự nhiên: trong mạng nhện, một số loài hoa, các nhánh xoắn của thiên hà, hệ thần kinh trong giác mạc, bão nhiệt đới, vỏ của các loài thân mềm, vỏ ốc sên và còn nhiều nữa.

Hình ảnh minh họa xoắn ốc logarithm trong tự nhiên. Nguồn: Manabie Vietnam
Jacob Bernoulli giữ ghế trưởng khoa Toán Đại học Basel từ năm 1695 cho đến khi ông qua đời năm 1705. Trên bia mộ của ông ngoài tên tuổi và công trạng, người ta có khắc hình một đường cong xoắn ốc logarithm (đáng tiếc rằng, do sự nhầm lẫn với đường xoắn ốc Archimedean nên đã khắc sai hình dạng) cùng với dòng chữ "eadem mutata resurgo" (Tôi sẽ trỗi dậy như cũ mặc dù đã thay đổi)

Bia mộ của Jacob Bernoulli ở Basel
2. Johann Bernoulli

Johann (hay là John hay là Jean) (27 tháng 7 năm 1667 – 1 tháng 1 năm 1748) là em út của Jacob, nhỏ hơn Jacob 13 tuổi. Cũng như tất cả những người con khác, ông Nicolas Bernoulli cho các con học Triết học và Thần học, mong muốn chúng trở thành những người thượng lưu thành đạt.
Học xong Trung học năm 1683, Johann vào Đại học Basel học Y Khoa, tốt nghiệp Bác sĩ năm 1694 nhưng không hành nghề. Trong cùng thời gian ấy, Johann nhờ anh là Jacob dạy thêm Toán, lúc ấy Jacob đang là giáo sư Toán ở Đại học Basel.
Năm 1684, tạp chí Acta Eruditorum của thành phố Leipzig (Đức) đăng bài báo của nhà toán học Leibniz về Phương pháp mới tìm các cực đại và cực tiểu ( Nova Methodus pro Maximis et Minimis ) giới thiệu phép tính vi phân do ông phát minh ra. Hai anh em Bernoulli đọc bài báo nhưng không hiểu được ý nghĩa của bài đó, Jacob liền viết thư cho Leibniz đề nghị được giải thích thêm. Không may lúc đó Leibniz lại sang du lịch nước Ý. Đợi mãi không có thư trả lời, Jacob liền nói với em:
Muốn hiểu được bài báo đó, tốt nhất là chúng ta tự tìm hiểu lấy!
Johann tán thành. Thế là hai anh em cùng bắt tay vào nghiên cứu.

Bức tranh anh em nhà Bernoulli: Jean (Johann) Benoulli (1667-1748) ở bên tay phải và Jacques (Jacob) Bernoulli (1654-1705) ở bên tay trái. Nguồn: Science Photo Library
Với sự giúp đỡ của Jacob, chẳng bao lâu Johann có thể tự một mình đọc được các tác phẩm của Leibniz, rồi tự nghiên cứu và phát triển thêm, đặc biệt là lý thuyết và kỹ thuật về phép tính vi-tích phân, một ngành Toán đang còn rất mới mẻ lúc bấy giờ. Jacob mau chóng nhận ra rằng em mình có một năng khiếu Toán rất đặc biệt và mình không có gì để dạy thêm cho Johann nữa.
Rồi hai anh em hợp tác cùng nghiên cứu một số vấn đề. Nhưng sự hợp tác ấy mau chóng tan vỡ vì những sự tranh cãi đôi khi ra ngoài phạm vi Toán học. Cái tôi của Jacob và Johann quá lớn. Cả hai không còn nhân nhượng nhau nữa, kể cả một số vấn đề thuộc phạm vi gia đình.
Nếu bỏ qua cá tính và những tai tiếng do quan hệ đối xử với Jacob, thì Johann là một nhà Toán học xuất sắc. Những gì ông làm được cho Toán học, đặc biệt cho phép tính vi-tích phân còn phong phú hơn cả Jacob nữa. Chính Johann Bernoulli là người đã dạy Toán cho Euler sau này tại Đại học Basel.
Dòng chảy những ý tưởng toán học vẫn không ngừng tuôn trào từ Johann Bernoulli. Năm 1694, ông đã xem xét hàm số
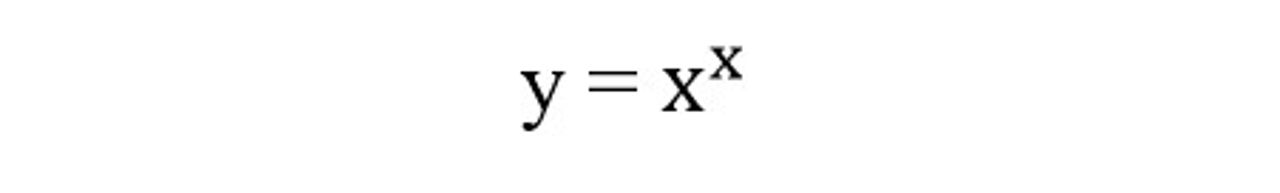
(10)
và nghiên cứu các chuỗi bằng phương pháp tích phân từng phần. Đối với Bernoulli, tích phân đơn giản chỉ là phép toán ngược lại của đạo hàm, và với cách tiếp cận này, ông đã đạt được nhiều thành công trong việc giải các phương trình vi phân. Ông đã tính tổng các chuỗi, đồng thời khám phá các định lý cộng cho các hàm lượng giác và siêu lượng giác thông qua các phương trình vi phân mà chúng thỏa mãn.
Những đóng góp xuất sắc này cho toán học đã được đền đáp xứng đáng vào năm 1695 khi ông nhận được hai lời mời đảm nhiệm chức danh giáo sư. Một là tại Đại học Halle, và một là ghế giáo sư toán học tại Đại học Groningen. Ghế giáo sư sau được trao cho Johann Bernoulli theo sự tiến cử của Huygens, và đây chính là vị trí mà ông vui mừng nhận lời – một phần quan trọng là vì điều đó giúp ông có được địa vị ngang bằng với người anh trai Jacob, người lúc ấy đang dần trở nên cực kỳ ganh tị trước những thành tựu của Johann.
Một điều thú vị là, tuy Johann được bổ nhiệm vào ghế giáo sư toán học, nhưng trong thư bổ nhiệm có nhắc đến kỹ năng y học của ông và cho phép ông hành nghề y tại Đại học Groningen nếu ông muốn.

Đại học Groningen, Hà Lan – Một trong những trường Đại học lâu đời nhất thế giới
Khi còn giữ ghế giáo sư tại Groningen, Johann Bernoulli đã quyết đấu với người anh trai của mình trong một cuộc đấu trí toán học thú vị. Bài toán đường đoản thời (brachistochrone curve) cho thấy tài năng và cá tính “kênh kiệu” của Johann Bernoulli. Trong số báo Acta Eruditorum tháng 6 năm 1696, Johann đăng thông báo sau đây:
Tôi, Johann Bernoulli, gửi những lời này tới những nhà Toán học xuất sắc nhất thế giới. Không có gì thu hút những con người thông minh bằng bài toán thử thách mà lời giải của họ sẽ làm cho họ nổi tiếng và lưu danh lại cho đời sau. Tôi hy vọng sẽ thu hút được sự chú ý của giới Khoa học trong đó có những nhà Toán học giỏi nhất của thời đại chúng ta như là Pascal và Fermat của thế hệ trước. Bài toán của tôi sẽ cho họ thể hiện phương pháp và tài năng của họ. Nếu họ gởi lời giải tới tôi, tôi sẽ đánh giá và công bố sự xứng đáng của họ.
Và đây là bài toán của Johann Bernoulli:
"Cho hai điểm A và B nằm trong mặt phẳng thẳng đứng P (A cao hơn B). Hãy xác định đường nối hai điểm A và B và nằm trong mặt phẳng P sao cho một điểm chỉ chịu trọng lực chạy từ A đến B trong thời gian ngắn nhất."
Bài toán "Brachistochrone", xuất phát từ tiếng Hу Lạp: Brachistos có nghĩa là “ngắn nhất” và chronos có nghĩɑ là “thời gian”. Tiếng Việt có sách gọi là “đoản thời”. Phân biệt với bài toán đường "đẳng thời" (Isochrone) là bất kỳ khởi hành ở điểm nào, cũng sẽ đạt điểm đáy trong cùng một thời gian như nhau dưới tác dụng của trọng lực, thì đường "đoản thời" (Brachistochrone) lại là vật thể di chuyển nhanh nhất (mất ít thời gian nhất) từ một điểm đến một điểm khác, dưới tác dụng của trọng lực. (Tất nhiên cả hai bài toán đều bỏ qua ma sát).
Có 5 bài giải đúng được gửi tới, trong đó 4 bài giải từ những nhà Toán học đã thành danh: De L’Hôpital, Leibniz, Jacob Bernoulli và chính của Johann Bernoulli. Còn bài giải thứ năm của một người ghi là vô danh. Bài giải của người vô danh này được Johann ghi bên lề là “Ex ungue Leonem” (Nhận biết con sư tử qua móng vuốt của nó).
Qua cách viết, lập luận và tính toán, Johann đã nhận ra được lời giải của người ghi “vô danh” này chính là của Newton và sau này Newton cũng công nhận như vậy. Newton còn nói thêm rằng ông đã mất 12 tiếng đồng hồ để giải bài toán ấy. Lời giải cho bài toán này là một phần đường cycloid lật ngược.
Phương pháp giải bài toán đường đoản thời của Johann Bernoulli rất độc đáo. Nó làm cách mạng phép tính vi-tích phân của Leibniz để trở thành một phép tính mới: phép tính biến phân (Calculus of variations).
Phương trình vi phân mà ông chứng minh
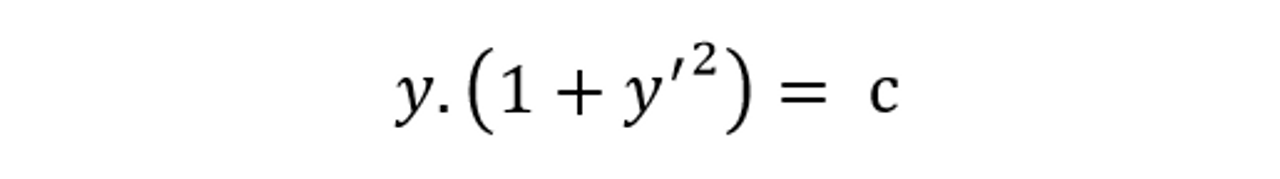
(11)
và ẩn của nó làm một hàm số (hàm số chúng ta cần tìm). Hàm số tìm được có đồ thị là một đường cong với tên gọi là Cycloid.
Điều đặc biệt trong cách chứng minh của Johann là ông đã liên hệ bài toán đơn thuần ban đầu là cơ học sang quang học. Cụ thể, để làm được điều này, ông viện dẫn đến nguyên lý của Fermat, rằng: ánh sáng luôn truyền theo con đường có thời gian đi ngắn nhất.
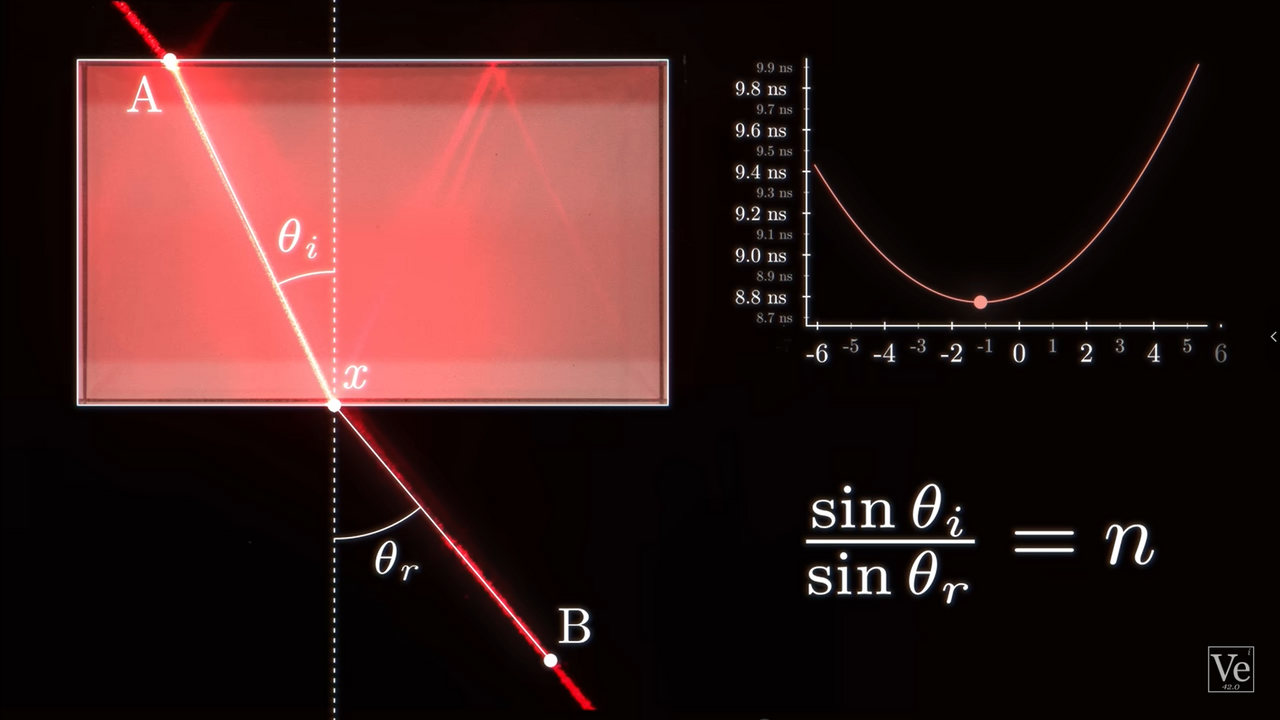
Nguyên lý Fermat (Fermat's principle). Nguồn: Veritasium
Về cách mà ông đã vận dụng nguyên lý Fermat thế nào để giải được bài toán, các bạn có thể tham khảo thêm ở phần đọc thêm dưới bài viết, nơi mình tổng hợp lại các chứng minh quan trọng của cả bài viết.
Để dễ hình dung bài toán, sau đây là mô phỏng chuyển động của viên bi theo những quỹ đạo khác nhau bằng phần mềm toán học Maple.
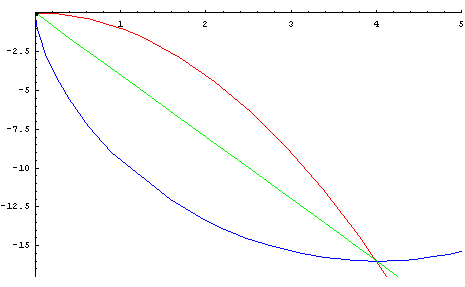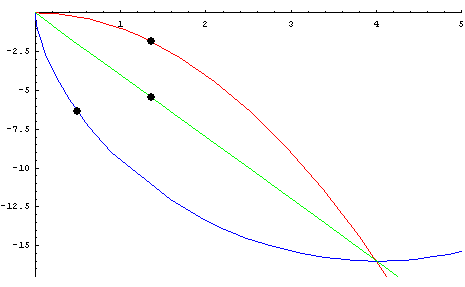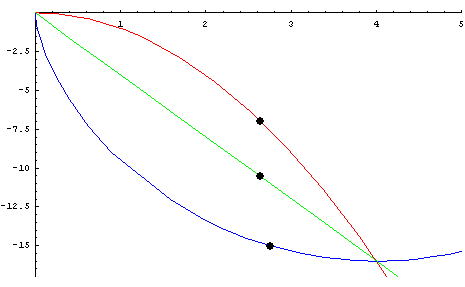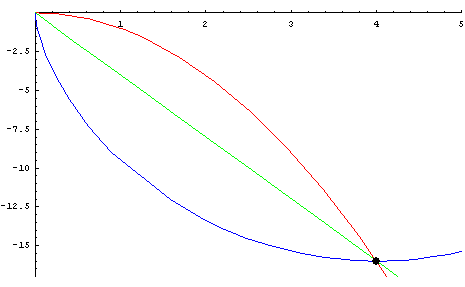
Nguồn: Blog TOÁN HỌC TƯƠI ĐẸP
Có thể thấy Đường đoản thời là đường màu xanh dương : ba hòn bi cùng thả ra tại một điểm, nhưng hòn bi chạy trên đường màu xanh dương (chính là đường cycloid) đến điểm cuối trước hai hòn bi kia.
Không quá cường điệu khi nói rằng việc tìm ra và chứng minh của Johann Bernouilli đó là một nghệ thuật về việc liên hệ độc đáo và thú vị để giải bài toán.
Tiếp theo ta đến với câu chuyện đầy gây cấn của Johann Bernoulli và nhà Toán học Guillaume de L’Hôpital (1661 - 1704). Một trong những lần tới Paris, Johann Bernoulli làm quen với Marquis de L’Hôpital – một trong những nhà toán học Pháp xuất chúng đương thời. L'Hôpital tỏ ra rất ngạc nhiên bởi tài năng của Bernoulli trẻ tuổi và cả nghệ thuật sử dụng phép tính vi phân và tích phân mà Leibniz lập ra.

Nhà toán học người Pháp Guillaume de l'Hôpital (1661 - 1704)
Biết mình còn thiếu những kiến thức toán học để hiểu phép tính vi phân và tích phân mà Leibniz lập ra, L’Hôpital đã thuê Johann với thù lao hậu hĩnh để Johann dạy mình những bí mật của phép tính mới. Khi phải quay trở về Basel, Johann hứa là sẽ không nói điều đó với ai và những bài giảng vẫn được tiếp tục qua thư từ qua lại.
Năm 1695, Johann Bernoulli gửi tới Hầu tước de L’Hôpital qui tắc nói rằng "nếu hai hàm số có đạo hàm và cả hai bằng 0 tại cùng một điểm, và nếu giới hạn tỷ số hai đạo hàm ấy tồn tại tại điểm ấy, thì giới hạn của tỷ số hai hàm số bằng giới hạn tỷ số hai đạo hàm tại điểm ấy". Diễn tả quy tắc ấy thành công thức như sau:
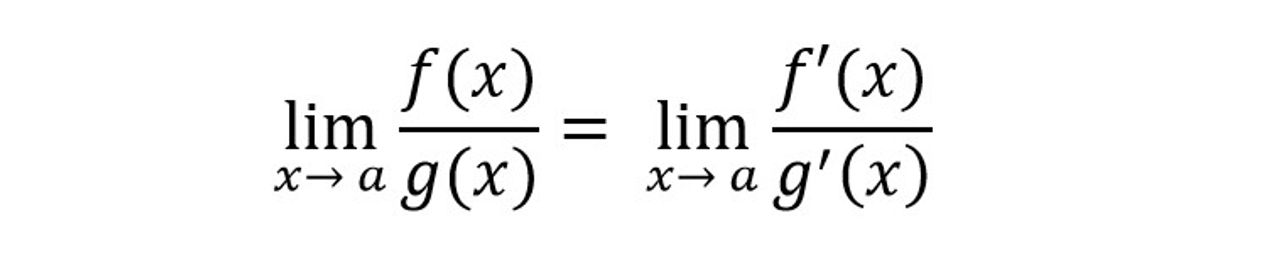
(11)
Về sau quy tắc này có trong phép tính vi-tích phân mà mọi sinh viên đều biết dưới tên gọi là quy tắc L’Hôpital.
Johann sao chép lại các bức thư vì muốn viết bài giảng về giải tích. Thế nhưng học trò thì đã nhanh chân hơn thầy. Sử dụng các bài giảng của Johann, năm 1696 L'Hôpital công bố công trình đầu tiên về phép tính vi phân Analyse des infiniment petits pour l'intelligence des lignes courbes (Giải tích các đại lượng vô cùng bé để khảo sát các đường cong).

Analyse des infiniment petits, puor l’intelligence des lignes courbes
Johann im lặng giống như đã hứa với L’Hôpital và không yêu cầu câu nhận quyền tác giả. Nhưng bằng cách riêng, ông than phiền, các phát minh của L’Hôpital là ăn cắp bản quyền một cách trơ tráo. Trong bức thư gửi Leibniz năm 1698, Bernoulli viết:
“Ngoại trừ một số trang thì tất cả phần còn lại là ông ta nhận được từ tôi qua thư […]. Ưu điểm của ông ta nằm ở chỗ ông ta đã sắp xếp theo trật tự và trình bày một cách cẩn thận bằng tiếng Pháp những thứ lộn xộn mà tôi đã viết cho ông ấy bằng tiếng Pháp hoặc tiếng La tinh”.
Mãi sau khi L’Hôpital mất vào năm 1704, Bernoulli mới đòi lại được một chút những gì đã mất bằng cách công bố nhiều kết quả của mình, trong đó có quy tắc L’Hôpital .
Những dấu hiệu đầu tiên cho thấy Johann có thể đã đúng phải đến tận năm 1922, khi người ta tìm thấy trong thư viện của Basel, giáo trình của Johann Cálculo differential (Phép tính vi phân); nó chưa từng được công bố. Nếu so sánh với quyển sách của L’Hôpital thì sẽ thấy rõ về bản chất chúng là một.
Kết luận rõ ràng xuất hiện vào năm 1955 khi bức thư đầu tiên giữa Johann và L’Hôpital được tìm thấy. Người ta phát hiện ra lời đề nghị lạ lùng mà L’Hôpital gửi cho Johann Bernulli trong bức thư gửi vào ngày 17 tháng 3 năm 1694.
“Tôi rất sẵn lòng gửi cho ngài khoảng 300 Livre bắt đầu từ ngày 1 tháng 1 năm nay; tôi sẽ gửi ngay 200 Livre trong nửa đầu năm cho phần khái quát mà ngài đã gửi cho tôi; còn 150 Livre nữa tôi sẽ gửi trong nửa cuối của năm và mọi thứ sẽ tiếp tục như thế. Tôi hứa rằng số tiền này trong thời gian sắp tới sẽ tăng lên vì tôi biết nó là rất ít; và tôi sẽ làm nó ngay khi công việc của tôi đạt kết quả tốt đẹp… Quả là gàn dở khi làm mất thời gian của ngài, nhưng tôi khẩn thiết đề nghị ngài thỉnh thoảng hãy dành cho tôi một vài tiếng để trả lời các câu hỏi của tôi và hãy gửi cho tôi những phát minh của mình, với điều kiện là không được công bố chúng với ai. Tôi cũng sẽ hứa là không gửi bản sao chép những tài liệu này cho Varignon hay bất kỳ người nào khác, bởi vì tôi không thích điều đó. Hãy trả lời tôi nhé!”.
Mặc dù thư hồi âm của Bernoulli không được tìm thấy, nhưng dễ hiểu là ông đã đồng ý thỏa thuận (không có gì ngạc nhiên nếu để ý rằng khi đó Johann mới 24 tuổi và đang không có việc làm). Trong những bức thư tiếp theo Bernoulli có trả lời thư và những câu hỏi của L’Hôpital . Một trong những bức thư ấy chứa công thức L’Hôpital . Ngoài ra những ví dụ mà Bernoulli đưa ra gần như trùng khớp với những ví dụ mà L’Hôpital về sau in trong quyển sách của mình. Nhưng cũng phải thừa nhận là L’Hôpital đã sửa vài lỗi của Bernoulli, ví dụ như Bernoulli cho rằng tích phân của hàm là hữu hạn.
Năm 1713, Johann Bernoulli tham dự vào cuộc tranh luận giữa Newton và Leibniz về vấn đề ai là người đầu tiên phát minh ra phép tính vi-tích phân.
Trong cuộc tranh cãi này hai anh em Jacob và Johann Bernoulli hoàn toàn ủng hộ Leibniz, nhất là Johann ủng hộ nhiệt tình, phản bác tích cực cáo buộc cho rằng Leibniz đạo ý tưởng của Newton do hầu hết những nhà Toán học đương thời của Anh đưa ra. Chính bài toán đường đoản thời mà Johann thách đố có dụng ý cho thấy ưu thế của phép tính vi-tích phân khai triển theo cách của Leibniz so với phương pháp vi-tích phân khai triển từ khái niệm chuyển động (fluxion: vận tốc) theo cách của Newton.
Ngoại trừ người vô danh (tức là Newton), không có một người nào theo phương pháp của Newton giải được bài toán ấy. Điều này không những xác nhận ưu thế của phép tính vi-tích phân của Leibniz mà còn cho thấy Leibniz là người sáng lập ra phép tính vi-tích phân một cách hoàn toàn độc lập với Newton.
Năm 1705, Jacob Bernoulli qua đời, Johann trở về Đại học Basel và sau đó được mời giữ chức trưởng khoa, thay thế cho người anh cả của mình. Ông ở đó cho đến cuối đời.
Johann Bernoulli đã đạt được danh tiếng lớn trong suốt cuộc đời mình. Ông được bầu làm viện sĩ của các viện hàn lâm Paris, Berlin, London, St Petersburg và Bologna. Mặc dù hầu hết các thành tựu của ông dường như có một số loại xung đột đằng sau chúng, nhưng ông vẫn là một nhân vật rất quan trọng trong lịch sử nhân loại. Ông được biết đến với cái tên "Archimedes of his age" (Archimedes của thời đại mình) và điều này thực sự được khắc trên bia mộ của ông.

3. Daniel Bernoulli

Johann Bernoulli có ba người con trai, kể theo thứ tự từ lớn đến nhỏ là Nicolas II (1687– 1759), Daniel (1700 – 1782) và Johann II (1710 – 1790). Cả ba đều là những nhà Toán học có tiếng, nhưng Daniel Bernoulli là xuất sắc hơn cả.
Daniel sinh tại Groningen, Hà Lan, tháng 2 năm 1700. Là một nhà Toán học xuất sắc và nổi tiếng nhưng Johann Bernoulli không muốn các con theo con đường của mình. Ông hướng các con vào con đường thương mại với lời giải thích là Toán không thể nào đem lại sự giàu có. Nhưng cả ba người con là Nicolas II, Daniel và Johann II đều chống lại ý muốn đó. Daniel thỏa thuận với cha chọn con đường như cha mình: học Y Khoa, nhưng rồi cũng như cha, Daniel không hành nghề. Ông tự học Toán, học Vật lý, học qua trao đổi và tranh luận với nhiều nhà Khoa học ở Ý, Đức và Pháp.
Từ 1725 đến 1757, ông thắng tổng cộng 10 giải thưởng của Viện Hàn Lâm Khoa học Paris, hầu hết các đề tài đều liên qua đến Toán học áp dụng vào Thiên văn, vào Thủy động học, vào Hải hành trên biển, vào Từ học.
Năm 1734 Daniel và cha của mình – nhà Toán học Johann Bernoulli - cùng được giải thưởng của Hàn Lâm Viên Khoa học Paris. Johann tức giận và không bằng lòng chia giải thưởng với Daniel vì cho rằng Daniel “đạo” ý tưởng của ông. Sau vụ này, ông tuyên bố không muốn thấy Daniel trong nhà ông nữa.
Johann Bernoulli không chỉ cạnh tranh gay gắt với người anh trai ruột thịt là Jacob Bernoulli nữa, mà thậm chí còn đố kị, ganh đua nhằm giành quyền ưu tiên là tác giả gốc công trình toán học qua tác phẩm Hydraulica trước chính con trai mình. Các nghiên cứu lịch sử đã xác nhận Johann thực sự là tác giả cuốn sách giải tích của de L’Hôpital, nhưng cũng chỉ ra rằng tuyên bố của ông về việc xuất bản Hydraulica trước khi Daniel viết Hydrodynamica là hoàn toàn sai sự thật.
Giải thưởng năm 1740 Daniel chia cùng với Euler và Mac Laurin trên đề tài dùng lý thuyết của Newton để nghiên cứu về thủy triều do sức hút của mặt trăng và mặt trời.

Ấn bản đầu tiên của cuốn Exercitationes Quaedam Mathematicae và cuốn Hydrodynamica.
Sau khi cuốn Exercitationes Quaedam Mathematicae được xuất bản, tài năng của Daniel được giới Khoa học biết tới. Năm 1725, theo lời giới thiệu của Leibniz, nữ hoàng Catherine I của Nga mời Daniel và người anh trai là Nicolas II (1695 – 1726) sang Nga tổ chức và điều hành ngành Toán của Viện hàn lâm khoa học Saint Petersburg mới được thành lập. Vừa mới hơn một năm, Nicolas II chết vì bệnh lao. Năm 1727, một ngôi sao đang lên còn rất trẻ (mới 20 tuổi) là bạn thân của hai anh em nhà Bernoulli và là học trò xuất sắc nhất của Johann Bernoulli tên là Leonhard Euler (1707 – 1783) sang thay thế vị trí của Nicolas II.

Viện hàn lâm khoa học Saint Petersburg
Vốn đã biết tiếng ông qua các công trình khoa học, tại đây các bạn đồng nghiệp khoa học người Nga đón tiếp ông nhiệt thành như những người anh em thân quen từ trước. Thời gian trôi, những tưởng chỉ sống ở đây một thời gian ngắn, nào ngờ ông đã sống suốt tám năm dòng, xa nước xa nhà. Chính trong thời gian này, bằng lao động miệt mài, Daniel Bernoulli đã tìm ra định luật nổi tiếng mang tên ông, đặt nền móng cho môn cơ học chất lỏng và chất khí.
Trong tất cả các vật tồn tại trên thế giới, nhà bác học Daniel Bernoulli quan tâm nhiều nhất đến dòng nước. Nước cuồn cuộn ngầu bọt qua hai bờ sông để lại những xoáy nước hun hút rợn người. Có lúc dòng sông hung hãn phá vỡ đê kè gây ra những nạn lụt hao người tốn của. Nước chảy qua sông máng, đường ống, cống ngầm vào đồng tưới tắm mùa màng. Vậy nước chảy như thế nào, “hành vi”, “tính cách”, “sức mạnh của nước khi chảy có thay đổi gì không? Tất cả những vấn đề đó đã cuốn hút toàn bộ tâm trí, thời gian và sức lực của nhà bác học. Trong thư gửi cho chánh văn phòng Viện hàn lâm ông viết:
“Đã sáu tháng nay tôi bắt tay vào viết một luận văn đầy đủ về các định luật chuyển động của nước... Tâm trí tôi bị choán bởi những tư tưởng kỳ diệu và tôi xin được miễn các công việc khác để có thể kết thúc công trình như tôi mong muốn”.
Trong tác phẩm Hydrodynamica vào năm 1738 của mình, ông trình bày về nguyên lí và phương trình nổi tiếng mang tên ông. Đó là nguyên lý Bernoulli áp dụng được cho nhiều loại chất lưu. Dựa vào sự bảo toàn năng lượng của dòng chất lưu khi chuyển động, Bernoulli đã thiết lập một phương trình mô tả trạng thái chuyển động của một dòng chất lưu lý tưởng chảy ổn định trong một ống dòng:

Nguồn: Physiad - Tạp chí vật lý
Điều kiện khảo sát và áp dụng:
+ Dòng chảy là ổn định, không có xoáy. Vận tốc của chất lưu ở mỗi vị trí không thay đổi theo thời gian.
+ Chất lỏng là không nhớt, tức là chuyển động của chất lỏng không có ma sát giữa các lớp chất lỏng và giữa chất lỏng với thành bình nên không gây ra mất mát năng lượng.
+ Chất lưu không bị nén, mật độ chất lưu không đổi.
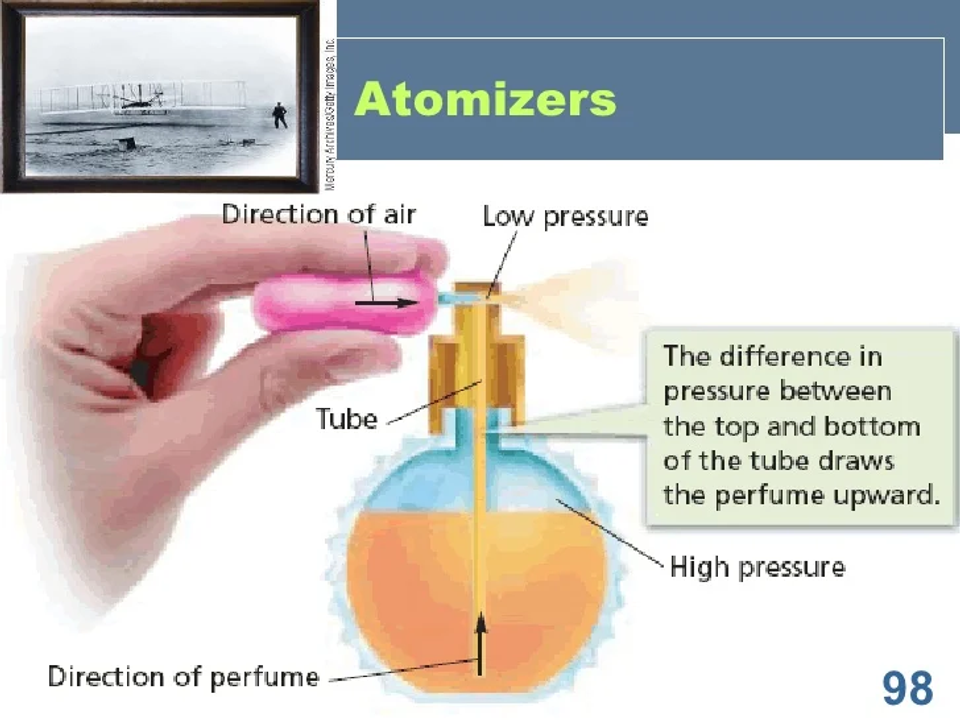
Để hiểu định luật Bernoulli trong thực tiễn, chẳng cần phải đâu xa, ta hãy vào một hiệu cắt tóc bất kỳ và quan sát cái bình bơm nước hoa một cơ cấu thủy lực đơn giản nhất, thiết kế căn cứ vào định luật Bernoulli. Ta có thể gọi đây là hiện tượng Venturi là hệ quả của phương trình Bernoulli.
Thế nhưng, định luật Bernoulli không phải lúc nào cũng có tác dụng tốt. Vào năm 1912, chiếc tàu biển RMS Olympic đang chạy trên mặt biển và cách nó chừng một trăm mét, chiếc thiết giáp hạm HMS Hawke nhỏ hơn nó nhiều, cũng đang lao đi hầu như song song với nó. Khi hai con tàu đi đến một ví trí gần như ngang hàng nhau thì xảy ra một chuyện hết sức bất ngờ: chiếc thiết giáp hạm tự nhiên trở quẻ, quay ngoắt đầu về phía con tàu lớn, rồi cưỡng lại tay lái và lao thẳng vào con tàu lớn. Kết quả là hai tàu húc phải nhau. Mũi tàu HMS Hawke đâm ngay vào tàu RMS Olympic mạnh đến nỗi sườn tàu RMS Olympic thủng một mảng lớn.

Hình ảnh của HMS Hawke và RMS Olympic sau vụ va chạm. Nguồn Wikipedia
Nguyên nhân của hiện tượng này có thể giải thích dựa vào định luật Bernoulli. Thật thế, khi hai con tàu đi song song thì phần biển ở giữa chúng giống như một dòng sông nhỏ. Trong các con sông thông thường thì bờ sông không chuyển động, còn ở đây thì ngược lại, nước không chuyển động mà bờ sông lại chuyển động. Những tác dụng của các lực thì chẳng vì thế mà thay đổi chút nào: ở phần hẹp của con sông di động này, nước ép vào thành yếu hơn so với ở khoảng không gian xung quanh tàu. Nói cách khác, hai sườn tàu đối diện nhau chịu một áp suất của nước nhỏ hơn so với áp suất ở phần ngoài tàu. Thành thử hai con tàu thế tất phải chuyển động hướng vào nhau và dĩ nhiên con tàu nhỏ lệch hướng chuyển động rõ rệt hơn, còn con tàu lớn thì hầu như vẫn chạy theo đường cũ.
Như vậy, những con tàu lớn khi phóng nhanh gần những con tàu nhỏ thường gây ra một lực hút rất mạnh, do tác dụng hút của dòng nước chảy. Điều này còn có thể vận dụng để giải thích sự nguy hiểm của dòng nước xiết đối với người đang tắm, tác dụng hút của những dòng nước xoáy, hay đoàn xe lửa lao nhanh đối với những người đứng cạnh đường tàu.
Ngoài ra nguyên lý Bernoulli còn là người bạn tri thức đồng hành với các phi công. Nguyên lý Bernoulli như ta đã biết là một khái niệm cơ bản trong động lực học chất lưu, giải thích mối quan hệ giữa áp suất và vận tốc trong chất lưu. Nhưng điều này cũng được chứng minh có liên quan trực tiếp đến luồng không khí.
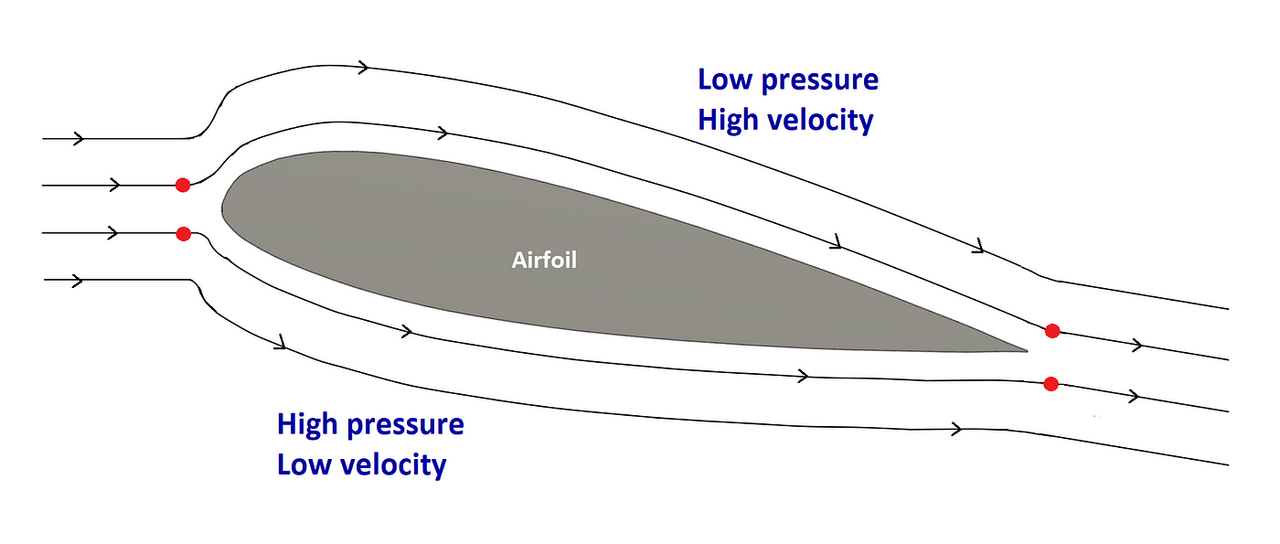
Khi không khí chảy qua cánh, nó chia thành hai luồng. Một luồng chảy qua bề mặt cong phía trên của cánh, luồng còn lại chảy bên dưới bề mặt phẳng phía dưới.
Theo Nguyên lý Bernoulli, khi không khí chảy qua bề mặt cong phía trên của cánh, vận tốc của nó tăng lên và áp suất của nó giảm xuống. Điều này tạo ra một vùng áp suất thấp hơn ở phía trên và áp suất cao hơn ở phía dưới cánh. Sự chênh lệch áp suất này tạo ra một lực hướng lên trên cánh, được gọi là lực nâng, cho phép máy bay cất cánh và ở trên không trung.
Thật thú vị khi nghĩ rằng hành động đơn giản của luồng không khí di chuyển trên bề mặt cong của cánh có thể tạo ra đủ lực nâng để giữ cho máy bay bay.
Lĩnh vực nổi tiếng tiếp theo mà ông đã góp phần là phát triển lý thuyết về bộ môn xác suất. Năm 1731, ở Saint-Petersburg, ông cho xuất bản cuốn Specimen Theoriae Novae de Mensura Sortis (Lý thuyết mới về tính toán các vận may rủi).

Trang đầu của cuốn Specimen Theoriae Novae de Mensura Sortis được đăng lạinăm 1738 trong Annals của Viện Hàn Lâm Saint-Petersburg.
Đây là tác phẩm nghiên cứu về xác suất trong đó Daniel có đề cập tới vấn đề số hy vọng (expected values) và cùng với người anh là Nicolas II đưa ra một bài toán sau này nổi tiếng với tên gọi nghịch lý Saint-Petersburg.
Hai anh em bắt đầu suy ngẫm về một trò chơi: tung một đồng xu liên tục “n” lần cho đến khi lần đầu tiên xuất hiện mặt ngửa. Nếu mặt ngửa xuất hiện lần đầu ở lần tung thứ n, người chơi sẽ nhận được 2 mũ n đô la. Vậy bạn sẵn sàng bỏ ra bao nhiêu tiền để tham gia trò chơi này? Mặc dù giá trị kỳ vọng của phần thưởng là vô hạn, vì:

Tất nhiên, không ai có vẻ sẵn sàng trả một khoản tiền khổng lồ như vậy để tham gia trò chơi này. Vì thế, Daniel Bernoulli đã giải quyết nghịch lý bằng cách giả định rằng mức độ hữu ích (utility) không tỉ lệ tuyến tính với phần thưởng, mà thay vào đó là một hàm lõm nghiêm ngặt là hàm logarit. Tiện ích gia tăng kỳ vọng của xổ số lúc này hội tụ về một giá trị hữu hạn:
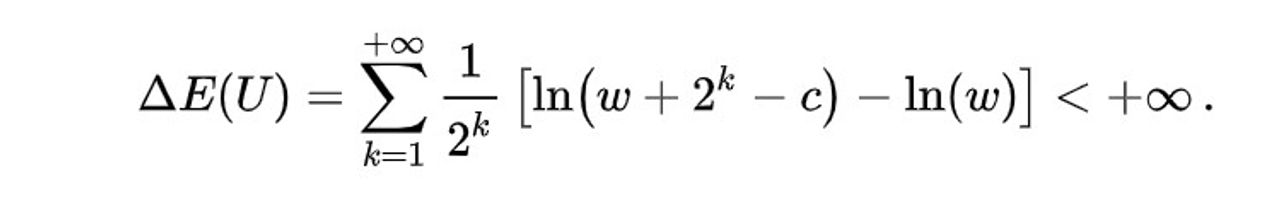
Công thức này đưa ra mối quan hệ ngầm định giữa tài sản của người chơi và số tiền họ nên sẵn sàng trả (cụ thể là bất kỳ giá trị c nào mang lại thay đổi tích cực trong tiện ích kỳ vọng).
Trong những năm cuối đời, Daniel tiếp tục nghiên cứu về phép tính vi-tích phân, cơ học, và nhiều vấn đề áp dụng Toán học vào Vật lý. Ông là thành viên của nhiều Hàn Lâm Viện Khoa học: Hàn Lâm Viện Paris, Hàn Lâm Viện Hoàng gia Anh, Hàn Lâm Viện Berlin, Hàn Lâm Viện Saint-Petersburg. Ông mất tại Basel năm 1782, thọ 82 tuổi.

Những thế hệ sau
Qua nhiều thế hệ, gia đình Bernoulli tiếp tục có thêm nhiều người theo đuổi truyền thống khoa học – toán học. Một số nhân vật tiêu biểu gồm có:
+) Johann II Bernoulli (1710–1790; còn được gọi là Jean), con trai của Johann, là nhà toán học và vật lý học.
+) Johann III Bernoulli (1744–1807; còn được gọi là Jean), con trai của Johann II, là nhà thiên văn học, địa lý học và toán học.
+) Jacob II Bernoulli (1759–1789; còn được gọi là Jacques), con trai của Johann II, là nhà vật lý và toán học.
+) Johann Jakob Bernoulli (1831–1913), nhà sử học nghệ thuật và khảo cổ học; nổi tiếng với tác phẩm Römische Ikonographie (từ năm 1882) về chân dung các hoàng đế La Mã.
+) Ludwig Bernoully (1873–1928), kiến trúc sư người Đức tại Frankfurt.
+) Hans Bernoulli (1876–1959), kiến trúc sư và người thiết kế khu nhà Bernoullihäuser ở Zurich và Grenchen (Thụy Sĩ).
+) Elisabeth Bernoulli (1873–1935), nhà hoạt động vì quyền bầu cử của phụ nữ và vận động chống nạn nghiện rượu.
Ngoài ra, gia đình Bernoulli còn có những cuộc hôn nhân nổi bật như:
+) Gia đình Curie (Pierre Curie là hậu duệ trực tiếp của Johann I).
+) Nhà văn Đức Hermann Hesse, người kết hôn với một hậu duệ trực tiếp của Johann I.
Kết
Mối quan hệ gia đình đầy cạnh tranh và đối kháng của nhà Bernoulli thường được cho là đã kìm hãm sự hợp tác và cản trở những thành công tiềm năng mà họ có thể đạt được nếu không quá khắc nghiệt với nhau. Tuy vậy, có lẽ chính sự ganh ghét và đố kỵ ấy lại trở thành chất xúc tác, thách thức và truyền cảm hứng để họ tạo nên những công trình toán học xuất sắc. Nếu Jacob không quá xuất sắc trong toán học và đồng thời cũng không quá ghen tị với em trai mình, thì Johann có lẽ đã không chịu cùng áp lực và động lực để vươn lên, vượt qua Jacob và ngược lại. Lập luận tương tự cũng đúng với mối quan hệ giữa Johann và con trai ông, Daniel.
Dù những mâu thuẫn, ganh đua và thù địch luôn tồn tại, không thể phủ nhận rằng gia đình Bernoulli là gia đình có nhiều thiên tài toán học nhất, với những đóng góp quan trọng và sâu sắc cho cộng đồng học thuật.
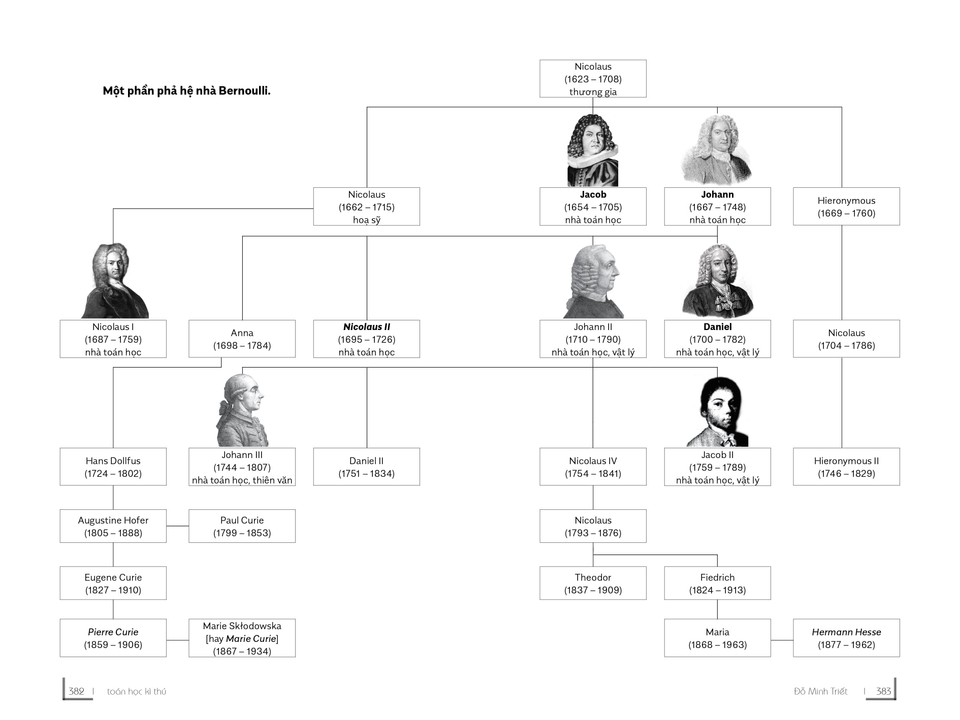
Tóm tắt gia phả Bernoulli qua bức hình. Nguồn: Sách "Toán học kì thú: Bạn biết bao nhiêu về toán?" - Đỗ Minh Triết
Các mục khác:
Nguồn tham khảo
[1] Abbott, David Ph.D. ed. "Bernoulli, Jacques & Bernoulli, Jean." The Biographical Dictionary of Sciences: Mathematics. New York: Peter Bedrick Books, 1985. p. 17.
[2] Bell, E.T. Men of Mathematics. New York: Simon and Schuster, Inc., 1937
[3] D Speiser, Daniel Bernoulli (1700-1782), Helvetica Physica Acta 55 (1982), 504-523.
[4] Leibniz GW. Briefwechsel zwischen Leibniz, Jacob Bernoulli, Johann Bernoulli und Nicolaus Bernoulli. (Hildesheim: Olms, 1971).
[5] Fellman, E. A. & J. O. Fleckenstein. "Bernoulli, Johann (Jean) I." Dictionary of Scientific Biography. New York: Charles Scribner's Sons, 1970. vol. 1, pp. 51-55.
[6] Graham, Daniel. Daniel Bernoulli and the St-Petersburg Paradox. 2005.
[7] Mukhopadhyay, Utpal. Bernoulli Brothers. Springer link. 2001.
[8] Sensenbaugh, Roger. "The Bernoulli Family." Great Lives from History Renaissance to 1900 Series. Englewood Cliffs, NJ: Salem Press, 1989. vol. 1, pp. 185-188.
[9] Hakfoort C. Optics in the age of Euler : conceptions of the nature of light, 1700-1795. (Cambridge: Cambridge University Press, 1995).
Đọc và xem thêm
P/s: Tình hình là mình chưa soạn xong tổng hợp đầy đủ các chứng minh tất cả các vấn đề có trong bài viết. Hi vọng sẽ kịp xong nhanh sớm để mọi người có thể tham khảo thêm.
Những nhà khoa học nổi bật khác nhà Bernoulli
Những nhà khoa học được nhắc trong bài viết

Quan điểm - Tranh luận
/quan-diem-tranh-luan
Bài viết nổi bật khác
- Hot nhất
- Mới nhất
